使用 C 的 DSA - 优先级队列

---

概述

优先级队列是比队列更专业的数据结构。与普通队列一样，优先级队列的方法相同，但有重大区别。在优先级队列中，项目按键值排序，因此键值最低的项目位于前面，键值最高的项目位于后面，反之亦然。因此，我们根据项目的键值为其分配优先级。值越低，优先级越高。以下是优先级队列的主要方法。

基本操作

• insert / enqueue - 将一个项目添加到队列的末尾。

• 删除/出队- 从队列前面删除一个项目。

优先级队列表示

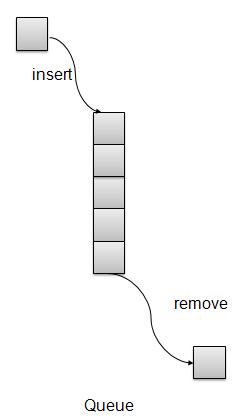
在本文中，我们将使用数组来实现队列。下面还有一些队列支持的操作。

• Peek - 获取队列前面的元素。

• isFull - 检查队列是否已满。

• isEmpty - 检查队列是否为空。

插入/入队操作

每当一个元素被插入到队列中时，优先级队列就会根据其顺序插入该项目。这里我们假设具有高价值的数据具有低优先级。

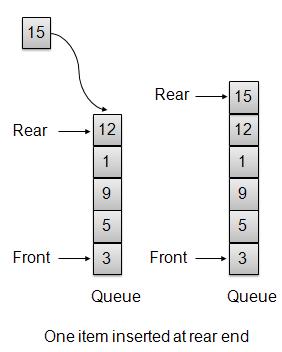
void insert(int data){
   int i =0;

   if(!isFull()){
      // if queue is empty, insert the data 
      if(itemCount == 0){
         intArray[itemCount++] = data;        
      } else {
         // start from the right end of the queue 
         for(i = itemCount - 1; i >= 0; i-- ){
            // if data is larger, shift existing item to right end 
            if(data > intArray[i]){
               intArray[i+1] = intArray[i];
            } else {
               break;
            }          
         }   
         // insert the data 
         intArray[i+1] = data;
         itemCount++;
      }
   }
}

删除/出队操作

每当要从队列中删除元素时，队列都会使用项目计数获取该元素。一旦元素被移除。项目数量减少 1。

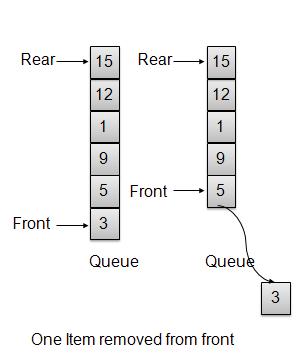
int removeData(){
   return intArray[--itemCount]; 
}

例子

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6

int intArray[MAX];
int itemCount = 0;

int peek(){
   return intArray[itemCount - 1];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   int i =0;

   if(!isFull()){
      // if queue is empty, insert the data 
      if(itemCount == 0){
         intArray[itemCount++] = data;        
      } else {
         // start from the right end of the queue 
         for(i = itemCount - 1; i >= 0; i-- ){
            // if data is larger, shift existing item to right end 
            if(data > intArray[i]){
               intArray[i+1] = intArray[i];
            } else {
               break;
            }            
         } 
         // insert the data 
         intArray[i+1] = data;
         itemCount++;
      }
   }
}
int removeData(){
   return intArray[--itemCount]; 
}
int main() {
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // ------------------
   // index : 0  1 2 3 4 
   // ------------------
   // queue : 12 9 5 3 1 
   insert(15);

   // ---------------------
   // index : 0  1 2 3 4  5 
   // ---------------------
   // queue : 15 12 9 5 3 1 
   if(isFull()){
      printf("Queue is full!\n");   
   }

   // remove one item 
   int num = removeData();
   printf("Element removed: %d\n",num);
   // ---------------------
   // index : 0  1  2 3 4 
   // ---------------------
   // queue : 15 12 9 5 3  

   // insert more items
   insert(16);

   // ----------------------
   // index :  0  1 2 3 4  5
   // ----------------------
   // queue : 16 15 12 9 5 3

   // As queue is full, elements will not be inserted. 
   insert(17);
   insert(18);

   // ----------------------
   // index : 0   1  2 3 4 5
   // ----------------------
   // queue : 16 15 12 9 5 3
   printf("Element at front: %d\n",peek());

   printf("----------------------\n");
   printf("index : 5 4 3 2  1  0\n");
   printf("----------------------\n");
   printf("Queue:  ");
   while(!isEmpty()){
      int n = removeData();           
      printf("%d ",n);
   }   
}

输出

如果我们编译并运行上面的程序，那么它将产生以下输出 -

Queue is full!
Element removed: 1
Element at front: 3
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 3 5 9 12 15 16