梅森增益公式

---

现在让我们讨论梅森增益公式。假设信号流图中有“N”条前向路径。信号流图的输入和输出节点之间的增益只不过是系统的传递函数。可以利用梅森增益公式来计算。

梅森增益公式为

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$

在哪里，

• C(s)是输出节点

• R(s)是输入节点

• T是 $R(s)$ 和 $C(s)$ 之间的传递函数或增益

• P _i是第 i 个^前向路径增益

$\Delta =1-(所有\: 个体\: 循环\: 收益的总和)$

$+(所有可能的两个非接触循环的增益乘积之和)$

$$-(总和\:增益\:乘积\:所有\:可能\:三个\:非接触\:循环)+...$$

Δ _{i是通过去除与第 i}^个前向路径接触的环路而从 Δ 获得的。

请考虑以下信号流图，以了解此处涉及的基本术语。

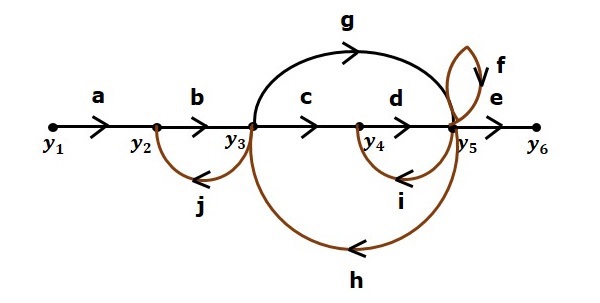
小路

它是从一个节点按照分支箭头方向到任意其他节点的分支遍历。它不应多次遍历任何节点。

示例- $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ 和 $y_5 \rightarrow y_3 \rightarrow y_2$

前进的道路

从输入节点到输出节点的路径称为前向路径。

示例- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 和 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。

前向路径增益

它是通过计算前向路径所有分支增益的乘积得到的。

示例- $abcde$ 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 的前向路径增益，abge 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow 的前向路径增益y_6$。

环形

从一个节点开始并在同一节点结束的路径称为循环。因此，它是一条封闭路径。

示例- $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_3 \rightarrow y_5 \rightarrow y_3$。

环路增益

它是通过计算一个循环的所有分支增益的乘积而获得的。

示例- $b_j$ 是 $y_2 \rightarrow y_3 \rightarrow y_2$ 的环路增益，$g_h$ 是 $y_3 \rightarrow y_5 \rightarrow y_3$ 的环路增益。

非接触式循环

这些是循环，不应有任何公共节点。

示例- 循环 $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_4 \rightarrow y_5 \rightarrow y_4$ 是非接触式的。

使用梅森增益公式计算传递函数

让我们考虑使用相同的信号流图来查找传递函数。

• 前向路径的数量，N = 2。

• 第一条前进路径是 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$。

• 第一个前向路径增益，$p_1 = abcde$。

• 第二条前进路径是 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。

• 第二个前向路径增益，$p_2 = abge$。

• 单独循环的数量，L = 5。

• 循环是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_3 \rightarrow y_5 \rightarrow y_3$、$y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$、$y_4 \rightarrow y_5 \rightarrow y_4$ 和 $y_5 \rightarrow y_5$。

• 循环增益为 - $l_1 = bj$、$l_2 = gh$、$l_3 = cdh$、$l_4 = di$ 和 $l_5 = f$。

• 两个非接触循环的数量 = 2。

• 第一个非接触循环对是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_4 \rightarrow y_5 \rightarrow y_4$。

• 获得第一个非接触循环对的乘积，$l_1l_4 = bjdi$

• 第二个非接触循环对是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_5 \rightarrow y_5$。

• 第二个非接触环路对的增益乘积为 - $l_1l_5 = bjf$

该信号流图中不存在更多数量（超过两个）的非接触环路。

我们知道，

$\Delta =1-(所有\: 个体\: 循环\: 收益的总和)$

$+(所有可能的两个非接触循环的增益乘积之和)$

$$-(总和\:增益\:乘积\:所有\:可能\:三个\:非接触\:循环)+...$$

代入上述方程中的值，

$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$

$\右箭头\Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$

不存在与第一条前向路径不接触的循环。

所以，$\Delta_1=1$。

类似地，$\Delta_2=1$。因为，没有与第二条前向路径不接触的循环。

代入梅森增益公式中的N = 2

$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$

$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$

将所有必要的值代入上式中。

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf }$$

$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf }$$

因此，传递函数是 -

$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$ $