DSP - 信号移位操作

---

移位意味着信号在时域（围绕 Y 轴）或幅度域（围绕 X 轴）的移动。因此，我们可以将平移分为两类，即时间平移和幅度平移，这些将在下面讨论。

时移

时移是指信号在时域中的移动。从数学上来说，它可以写成

$$x(t) \rightarrow y(t+k)$$

这个K值可以是正值，也可以是负值。根据k值的符号，我们有两种类型的移位，称为右移位和左移位。

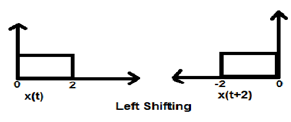
情况1（K > 0）

当 K 大于零时，信号在时域中向“左”移动。因此，这种类型的移位被称为信号的左移位。

例子

情况2（K<0）

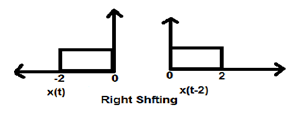
当 K 小于零时，信号在时域中向右移动。因此，这种类型的移位被称为右移位。

例子

下图显示了信号右移 2。

幅度转换

幅度偏移意味着信号在幅度域（绕 X 轴）的偏移。在数学上，它可以表示为 -

$$x(t) \rightarrow x(t)+K$$

这个K值可以是正值，也可以是负值。因此，我们有两种类型的幅移，随后将在下面讨论。

情况1（K > 0）

当 K 大于零时，信号沿 x 轴向上移动。因此，这种类型的换档被称为向上换档。

例子

让我们考虑一个信号 x(t)，其给出为：

$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

假设我们采用 K=+1，因此新信号可以写为 -

$y(t) \rightarrow x(t)+1$ 因此，y(t) 最终可以写为；

$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$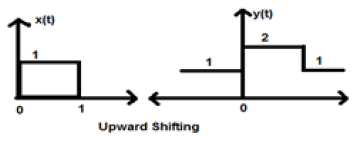

情况2（K<0）

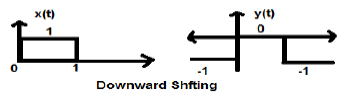
当 K 小于零时，信号会沿 X 轴向下移动。因此，称为信号下移。

例子

让我们考虑一个信号 x(t)，其给出为：

$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$

让我们取 K = -1，这样新信号可以写成：

$y(t)\rightarrow x(t)-1$ 因此，y(t) 最终可以写为；

$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$