设计与分析 - 插值搜索

插值搜索是二分搜索的改进变体。该搜索算法作用于所需值的探测位置。为了使该算法正常工作，数据收集应该是排序的形式并且均匀分布。

与线性搜索相比，二分搜索在时间复杂度上具有巨大的优势。线性搜索的最坏情况复杂度为 Ο(n)，而二分搜索的最坏情况复杂度为 Ο(log n)。

在某些情况下，可以提前知道目标数据的位置。例如，在电话簿的情况下，如果我们要搜索“Morpheus”的电话号码。在这里，线性搜索甚至二分搜索都会显得很慢，因为我们可以直接跳转到存储以“M”开头的名称的内存空间。

二分查找中的定位

在二分搜索中，如果未找到所需的数据，则列表的其余部分将分为两部分：较低部分和较高部分。搜索在其中任何一个中进行。

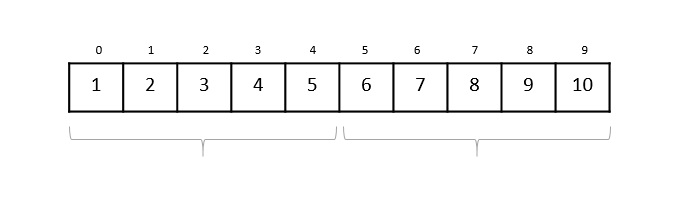
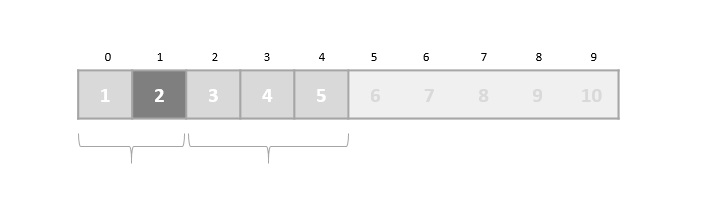
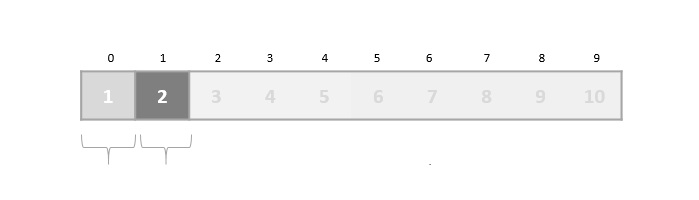
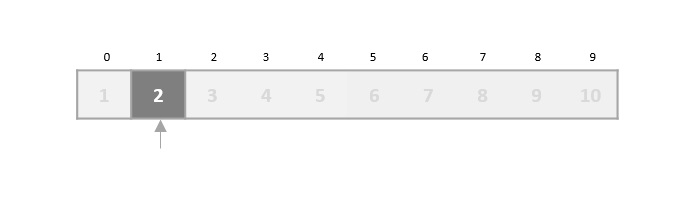
即使数据已排序，二分查找也无法探测所需数据的位置。

插补搜索中的位置探测

插值搜索通过计算探针位置来查找特定项目。最初，探测位置是集合中最中间项的位置。

插值搜索中的位置探测

如果发生匹配，则返回该项目的索引。要将列表分成两部分，我们使用以下方法 -

$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \右 )}{A\左 [ Hi \右 ]\, -\, A\左 [ Lo \右 ]}$

其中 -

A = list
Lo = Lowest index of the list
Hi = Highest index of the list
A[n] = Value stored at index n in the list

如果中间项大于该项，则在中间项右侧的子数组中再次计算探针位置。否则，将在中间项左侧的子数组中搜索该项。这个过程也在子数组上继续，直到子数组的大小减少到零。

插值搜索算法

由于它是现有 BST 算法的即兴改进，因此我们提到使用位置探测来搜索“目标”数据值索引的步骤 -

步骤 1 - 从列表中间开始搜索数据。

步骤 2 - 如果匹配，则返回该项目的索引，然后退出。

步骤 3 - 如果不匹配，则探测位置。

步骤 4 - 使用探测公式划分列表并找到新的中间项。

步骤 5 - 如果数据大于中间，则在更高的子列表中搜索。

步骤 6 - 如果数据小于中间，则在较低的子列表中搜索。

步骤 7 - 重复直到匹配。

伪代码

A → Array list
N → Size of A
X → Target Value

Procedure Interpolation_Search()

   Set Lo → 0
   Set Mid → -1
   Set Hi → N-1

   While X does not match
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if

      Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])

      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While
End Procedure

分析

在有利情况下，插值搜索算法的运行时间复杂度为Ο(log (log n))，而BST 的运行时间复杂度为Ο(log n) 。

例子

为了了解插值搜索中涉及的逐步过程，让我们看一个示例并解决它。

考虑下面给出的排序元素数组 -

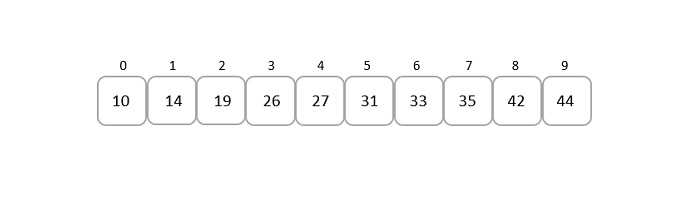
让我们搜索元素 19。

解决方案

与二分搜索不同，这种方法的中间点是使用以下公式选择的 -

$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \右 )}{A\左 [ Hi \右 ]\, -\, A\左 [ Lo \右 ]}$

所以在这个给定的数组输入中，

Lo = 0, A[Lo] = 10
Hi = 9, A[Hi] = 44
X = 19

应用公式找到列表中的中间点，我们得到

$mid\, =\, 0\, +\, \frac{\left ( 9\, -\, 0 \right )\ast \left ( 19\, -\, 10 \right )}{44\, -\, 10}$

$mid\, =\, \frac{9\ast 9}{34}$

$mid\, =\, \frac{81}{34}\,=\,2.38$

由于mid是索引值，因此我们只考虑小数的整数部分。即，中值=2。

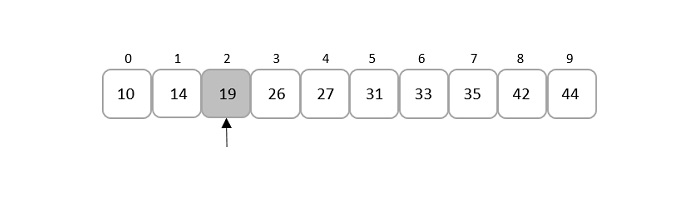
将给定的关键元素（即 19）与中间索引中存在的元素进行比较，发现两个元素都匹配。

因此，该元素位于索引 2 处。

例子

插值搜索是二分搜索的改进变体。该搜索算法作用于所需值的探测位置。为了使该算法正常工作，数据收集应该是排序且均匀分布的形式。

C C++ Java Python


#include<stdio.h>
#define MAX 10

// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
   int lo = 0;
   int hi = MAX - 1;
   int mid = -1;
   int comparisons = 1;
   int index = -1;
   while(lo <= hi) {
      printf("\nComparison %d \n" , comparisons ) ;
      printf("lo : %d, list[%d] = %d\n", lo, lo, list[lo]);
      printf("hi : %d, list[%d] = %d\n", hi, hi, list[hi]);
      comparisons++;
      
      // probe the mid point
      mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
      printf("mid = %d\n",mid);
      
      // data found
      if(list[mid] == data) {
         index = mid;
         break;
      } else {
         if(list[mid] < data) {
            
            // if data is larger, data is in upper half
            lo = mid + 1;
         } else {
            
            // if data is smaller, data is in lower half
            hi = mid - 1;
         }
      }
   }
   printf("\nTotal comparisons made: %d", --comparisons);
   return index;
}
int main(){
   
   //find location of 33
   int location = interpolation_search(33);
   
   // if element was found
   if(location != -1)
      printf("\nElement found at location: %d" ,(location+1));
   else
      printf("Element not found.");
   return 0;
}

输出

Comparison 1 
lo : 0, list[0] = 10
hi : 9, list[9] = 44
mid = 6

Total comparisons made: 1
Element found at location: 7


#include<iostream>
using namespace std;
#define MAX 10

// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
   int lo = 0;
   int hi = MAX - 1;
   int mid = -1;
   int comparisons = 1;
   int index = -1;
   while(lo <= hi) {
      cout << "\nComparison " << comparisons << endl;
      cout << "lo : " << lo << " list[" << lo << "] = " << list[lo] << endl;
      cout << "hi : " << hi << " list[" << hi << "] = " << list[hi] << endl;
      comparisons++;
      
      // probe the mid point
      mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
      cout << "mid = " << mid;
      
      // data found
      if(list[mid] == data) {
         index = mid;
         break;
      } else {
         if(list[mid] < data) {
            
            // if data is larger, data is in upper half
            lo = mid + 1;
         } else {
            
            // if data is smaller, data is in lower half
            hi = mid - 1;
         }
      }
   }
   cout << "\nTotal comparisons made: " << (--comparisons);
   return index;
}
int main(){
   
   //find location of 33
   int location = interpolation_search(33);
   
   // if element was found
   if(location != -1)
      cout << "\nElement found at location: " << (location+1);
   else
      cout << "Element not found.";
   return 0;
}

输出

Comparison 1
lo : 0 list[0] = 10
hi : 9 list[9] = 44
mid = 6
Total comparisons made: 1
Element found at location: 7


import java.io.*;
public class InterpolationSearch {
   static int interpolation_search(int data, int[] list) {
      int lo = 0;
      int hi = list.length - 1;
      int mid = -1;
      int comparisons = 1;
      int index = -1;
      while(lo <= hi) {
         System.out.println("\nComparison " + comparisons);
         System.out.println("lo : " + lo + " list[" + lo + "] = " + list[lo]);
         System.out.println("hi : " + hi + " list[" + hi + "] = " + list[hi]);
         comparisons++;
         
         // probe the mid point
         mid = lo + (((hi - lo) * (data - list[lo])) / (list[hi] - list[lo]));
         System.out.println("mid = " + mid);
         
         // data found
         if(list[mid] == data) {
            index = mid;
            break;
         } else {
            if(list[mid] < data) {
               
               // if data is larger, data is in upper half
               lo = mid + 1;
            } else {
               
               // if data is smaller, data is in lower half
               hi = mid - 1;
            }
         }
      }
      System.out.println("\nTotal comparisons made: " + (--comparisons));
      return index;
   }
   public static void main(String args[]) {
      int[] list = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
      
      //find location of 33
      int location = interpolation_search(33, list);
      
      // if element was found
      if(location != -1)
         System.out.println("\nElement found at location: " + (location+1));
      else
         System.out.println("Element not found.");
   }
}

输出

Comparison 1
lo : 0 list[0] = 10
hi : 9 list[9] = 44
mid = 6
Total comparisons made: 1
Element found at location: 7


def interpolation_search( data, arr):
   lo = 0
   hi = len(arr) - 1
   mid = -1
   comparisons = 1
   index = -1
   while(lo <= hi):
      print("\nComparison ", comparisons)
      print("lo : ", lo)
      print("list[", lo, "] = ")
      print(arr[lo])
      print("hi : ", hi)
      print("list[", hi, "] = ")
      print(arr[hi])
      comparisons = comparisons + 1

      #probe the mid point
      mid = lo + (((hi - lo) * (data - arr[lo])) // (arr[hi] - arr[lo]))
      print("mid = ", mid)

      #data found
      if(arr[mid] == data):
         index = mid
         break
      else:
         if(arr[mid] < data):
            
            #if data is larger, data is in upper half
            lo = mid + 1
         else:

            #if data is smaller, data is in lower half
            hi = mid - 1
   print("\nTotal comparisons made: ")
   print(comparisons-1)
   return index

arr = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
#find location of 33
location = interpolation_search(33, arr)

#if element was found
if(location != -1):
   print("\nElement found at location: ", (location+1))
else:
   print("Element not found.")

输出

Comparison  1
lo :  0
list[ 0 ] = 
10
hi :  9
list[ 9 ] = 
44
mid =  6

Total comparisons made: 
1

Element found at location:  7