设计与分析 - 指数搜索

指数搜索算法以输入数组的一个范围为目标，其中假定所需元素必须存在于该范围内，并在该特定的小范围上执行二分搜索。该算法也称为加倍搜索或手指搜索。

它类似于跳跃搜索，将排序后的输入分成多个块并进行更小规模的搜索。然而，在执行计算以划分块以及应用的较小规模搜索的类型（跳跃搜索应用线性搜索而指数搜索应用二分搜索）时会出现差异。

因此，该算法以 2 的幂指数跳跃。简单来说，搜索是在使用 pow(2, k) 划分的块上执行的，其中 k 是大于或等于 0 的整数。一旦位置 pow( 2、n)大于关键元素，则对当前块进行二分查找。

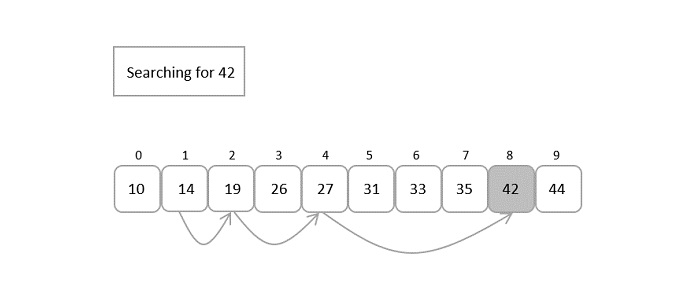
指数搜索算法

在指数搜索算法中，跳转从数组的第一个索引开始。因此，我们手动比较第一个元素作为算法的第一步。

步骤 1 - 将数组中的第一个元素与键进行比较，如果找到匹配则返回第 0 个索引。

步骤 2 - 初始化 i = 1 并将数组的第 i 个元素与要搜索的键进行比较。如果匹配则返回索引。

步骤 3 - 如果元素不匹配，则以 2 的幂指数方式跳转数组。因此，现在算法比较增量位置中存在的元素。

步骤 4 - 如果找到匹配项，则返回索引。否则，迭代重复步骤2，直到增量位置处的元素变得大于要搜索的关键字。

步骤 5 - 由于下一个增量具有比键更高的元素并且输入已排序，因此该算法对当前块应用二分搜索算法。

步骤 6 - 如果找到匹配，则返回键所在的索引；否则判定搜索不成功。

伪代码

Begin
   m := pow(2, k) // m is the block size
   start := 1
   low := 0
   high := size – 1 // size is the size of input
   if array[0] == key
      return 0
   while array[m] <= key AND m < size do
      start := start + 1
      m := pow(2, start)
      while low <= high do:
         mid = low + (high - low) / 2
         if array[mid] == x
            return mid
         if array[mid] < x
            low = mid + 1
         else
            high = mid - 1
   done
   return invalid location
End

分析

尽管它被称为指数搜索，但它并不以指数时间复杂度执行搜索。但众所周知，在这个搜索算法中，执行的基本搜索是二分搜索。因此，指数搜索算法的时间复杂度将与二分搜索算法的时间复杂度相同，O(log n)。

例子

为了更好地、以更简单的方式理解指数搜索算法，让我们使用指数搜索算法在示例输入数组中搜索元素 -

提供给搜索算法的排序输入数组是 -

让我们搜索给定数组中元素 81 的位置。

步骤1

将数组的第一个元素与关键元素 81 进行比较。

数组第一个元素是6，但要查找的关键元素是81；因此，由于没有找到匹配项，因此跳转从第一个索引开始。

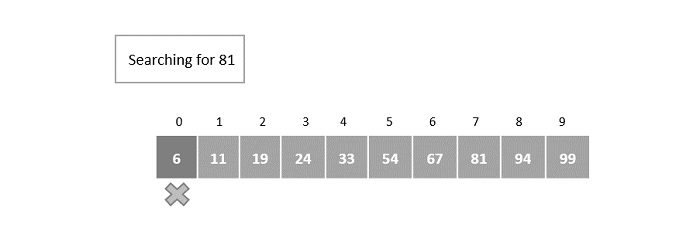
第2步

初始化 i = 1 后，将关键元素与第一个索引中的元素进行比较。这里，第一个索引中的元素与键元素不匹配。所以它再次以 2 的幂指数递增。

索引增加到 2 ^m = 2 ^{1 = 将第二个}索引中的元素与关键元素进行比较。

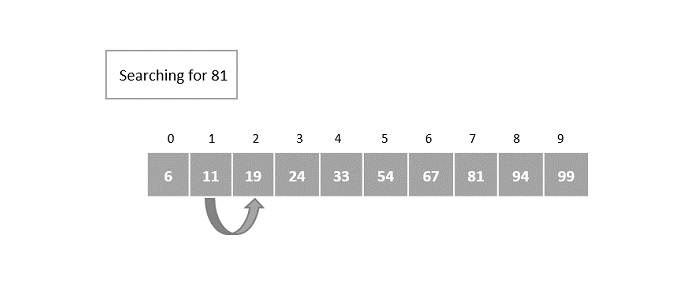
它仍然不匹配，因此再次递增。

步骤3

索引再次以 2 的幂递增。

2 ^{2 = 4 = 将第 4个}索引中的元素与关键元素进行比较，但尚未找到匹配项。

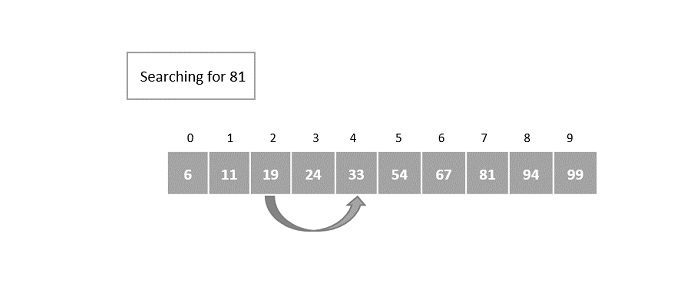
步骤4

该指数再次呈指数增长。这次将第 8 个索引中的元素与关键元素进行比较，没有找到匹配项。

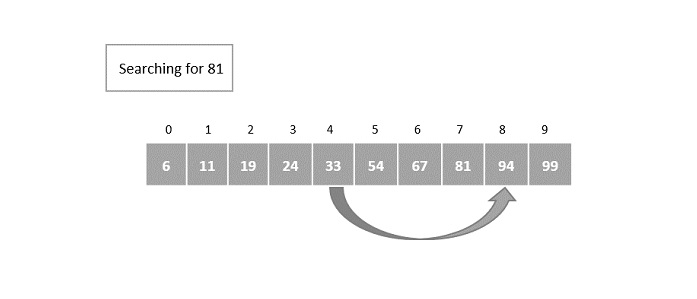
但是，第 8 个索引中的元素大于键元素。因此，二分搜索算法应用于当前元素块。

步骤5

当前元素块包括索引 [4, 5, 6, 7] 中的元素。

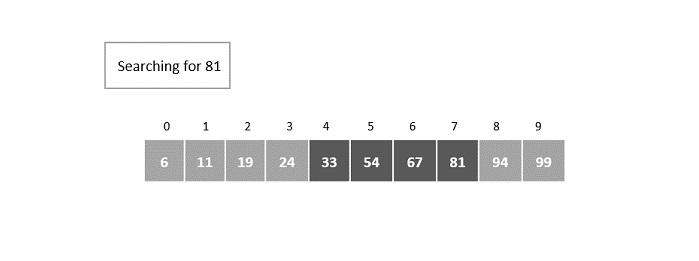
小规模二分搜索应用于该元素块，其中 mid 被计算为第 5^个元素。

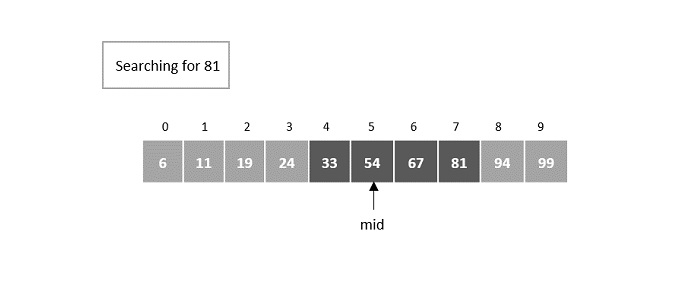
步骤6

在中间元素处未找到匹配项，并且表明所需元素大于中间元素。因此，搜索发生在块的右半部分。

现在中点被设置为第 6^个元素 -

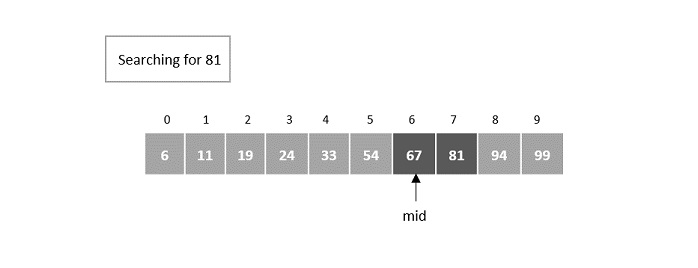
步骤7

^{在第 6个}元素处仍未找到该元素，因此它现在在中间元素的右半部分中搜索。

下一个 mid 被设置为第 7^个元素。

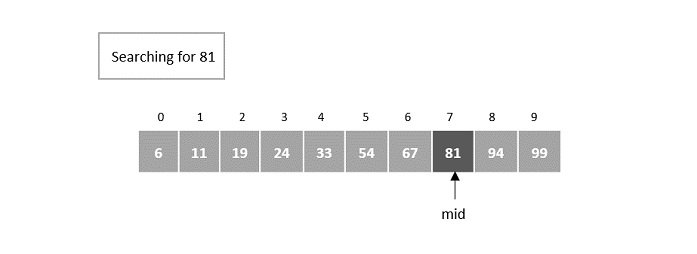
此处，该元素位于第 7^个索引处。

执行

在指数搜索算法的实现中，程序在每次指数跳跃时检查 2 的幂是否匹配。如果找到匹配，则返回元素的位置，否则程序返回不成功的搜索。

一旦指数跳跃处的元素变得大于关键元素，将对当前元素块执行二分搜索。

在本章中，我们将研究四种不同语言的指数搜索的实现。

#include <stdio.h>
#include <math.h>
int exponential_search(int[], int, int);
int main(){
   int i, n, key, pos;
   int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
   n = 10;
   key = 67;
   pos = exponential_search(arr, n, key);
   if(pos >= 0)
      printf("The element is found at %d", pos);
   else
      printf("Unsuccessful Search");
}
int exponential_search(int a[], int n, int key){
   int i, m, low = 0, high = n - 1, mid;
   i = 1;
   m = pow(2,i);
   if(a[0] == key)
      return 0;
   while(a[m] <= key && m < n) {
      i++;
      m = pow(2,i);
      while (low <= high) {
         mid = (low + high) / 2;
         if(a[mid] == key)
            return mid;
         else if(a[mid] < key)
            low = mid + 1;
         else
            high = mid - 1;
      }
   }
   return -1;
}

The element is found at 6

#include <iostream>
#include <cmath>
using namespace std;
int exponential_search(int[], int, int);
int main(){
   int i, n, key, pos;
   int arr[10] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
   n = 10;
   key = 67;
   pos = exponential_search(arr, n, key);
   if(pos >= 0)
      cout << "The element is found at " << pos;
   else
      cout << "Unsuccessful Search";
}
int exponential_search(int a[], int n, int key){
   int i, m, low = 0, high = n - 1, mid;
   i = 1;
   m = pow(2,i);
   if(a[0] == key)
      return 0;
   while(a[m] <= key && m < n) {
      i++;
      m = pow(2,i);
      while (low <= high) {
         mid = (low + high) / 2;
         if(a[mid] == key)
            return mid;
         else if(a[mid] < key)
            low = mid + 1;
         else
            high = mid - 1;
      }
   }
   return -1;
}

The element is found at 6

import java.io.*;
import java.util.Scanner;
import java.lang.Math;
public class ExponentialSearch {
   public static void main(String args[]) {
      int i, n, key;
      int arr[] = {6, 11, 19, 24, 33, 54, 67, 81, 94, 99};
      n = 10;
      key = 67;
      int pos = exponential_search(arr, n, key);
      if(pos >= 0)
         System.out.print("The element is found at " + pos);
      else
         System.out.print("Unsuccessful Search");
   }
   static int exponential_search(int a[], int n, int key) {
      int i = 1;
      int m = (int)Math.pow(2,i);
      if(a[0] == key)
         return 0;
      while(a[m] <= key && m < n) {
         i++;
         m = (int)Math.pow(2,i);
         int low = 0;
         int high = n - 1;
         while (low <= high) {
            int mid = (low + high) / 2;
            if(a[mid] == key)
               return mid;
            else if(a[mid] < key)
               low = mid + 1;
            else
               high = mid - 1;
         }
      }
      return -1;
   }
}

The element is found at 6

import math
def exponential_search(a, n, key):
   i = 1
   m = int(math.pow(2, i))
   if(a[0] == key):
      return 0
   while(a[m] <= key and m < n):
      i = i + 1
      m = int(math.pow(2, i))
      low = 0
      high = n - 1
      while (low <= high):
         mid = (low + high) // 2
         if(a[mid] == key):
            return mid
         elif(a[mid] < key):
            low = mid + 1
         else:
            high = mid - 1
   return -1
   
arr = [6, 11, 19, 24, 33, 54, 67, 81, 94, 99]
n = len(arr);
key = 67
index = exponential_search(arr, n, key)
if(index >= 0):
   print("The element is found at index: ", (index))
else:
   print("Unsuccessful Search")

The element is found at index:  6