宇宙学 - 角直径距离
在本章中,我们将了解什么是角直径距离以及它对宇宙学有何帮助。
对于现在的宇宙 -
$\Omega_{m,0} \: = \: 0.3$
$\Omega_{\楔形,0} \: = \: 0.69$
$\Omega_{rad,0} \: = \: 0.01$
$\Omega_{k,0} \: = \: 0$
到目前为止我们已经研究了两种类型的距离 -
本征距离 (lp) - 光子从源到我们的距离,即瞬时距离。
共动距离 (lc) - 不扩展空间中物体之间的距离,即共动参考系中的距离。
距离作为红移的函数
考虑一个在时间t 1辐射光子的星系,该光子在t 0被观察者检测到。我们可以将到星系的正确距离写为 -
$$l_p = \int_{t_1}^{t_0} cdt$$
设星系的红移为z,
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\压裂{1}{a}$$
$$\因此 \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$
现在,任意时刻t时星系的同动距离为 -
$$l_c = \frac{l_p}{a(t)}$$
$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$
就 z 而言,
$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$
有两种方法可以找到距离,如下 -
光通量-光度关系
$$F = \frac{L}{4\pi d^2}$$
其中d是源处的距离。
光源的角直径距离
如果我们知道光源的大小,它的角宽度就会告诉我们它与观察者的距离。
$$\theta = \frac{D}{l}$$
其中l是源的角直径距离。
θ是光源的角度大小。
D是源的大小。
考虑一个大小为 D 且角大小为dθ的星系。
我们知道,
$$d\theta = \frac{D}{d_A}$$
$$\因此 D^2 = a(t)^2(r^2 d\theta^2) \quad \因为 dr^2 = 0; \: d\phi ^2 \约 0$$
$$\右箭头 D = a(t)rd\theta$$
将r更改为r c,即星系的同移距离,我们有 -
$$d\theta = \frac{D}{r_ca(t)}$$
在这里,如果我们选择t = t 0,我们最终会测量到星系的当前距离。但D是在光子发射时测量的。因此,通过使用t = t 0,我们得到了到星系的更大距离,从而低估了它的大小。因此,我们应该使用时间t 1。
$$\因此 d\theta = \frac{D}{r_ca(t_1)}$$
将其与之前的结果进行比较,我们得到 -
$$d_\楔形 = a(t_1)r_c$$
$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \因为 1+z_1 = \frac{1}{a(t_1)}$$
所以,
$$d_\楔形 = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$
d A是物体的角直径距离。
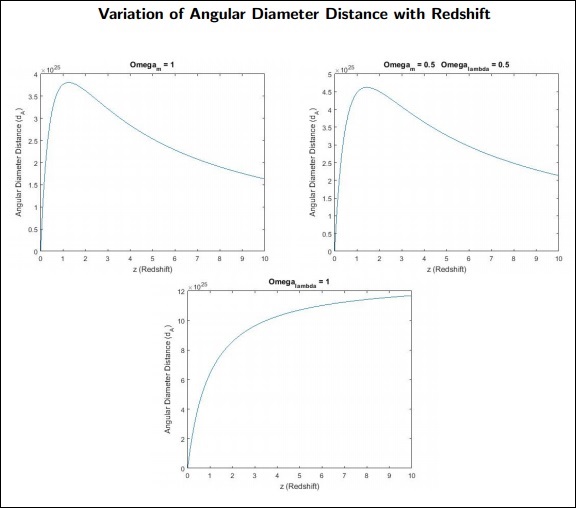
需要记住的要点
如果我们知道光源的大小,它的角宽度就会告诉我们它与观察者的距离。
适当的距离是光子从源到我们的距离。
同动距离是指在不膨胀的空间中物体之间的距离。
