雷达系统 - 延迟线消除器

---

在本章中，我们将了解雷达系统中的延迟线消除器。顾名思义，延迟线引入了一定量的延迟。因此，延迟线主要用于延迟线消除器，以引入脉冲重复时间的延迟。

延迟线消除器是一种滤波器，可消除从静止目标接收的回波信号的直流分量。这意味着，它允许从非静止目标（即移动目标）接收到的回波信号的交流分量。

延迟线消除器的类型

根据延迟线消除器中存在的延迟线的数量，延迟线消除器可以分为以下两种类型。

• 单延迟线消除器
• 双延迟线消除器

在后续部分中，我们将详细讨论这两个延迟线消除器。

单延迟线消除器

延迟线和减法器的组合称为延迟线消除器。它也称为单延迟线消除器。具有单延迟线消除器的MTI接收器的框图如下图所示。

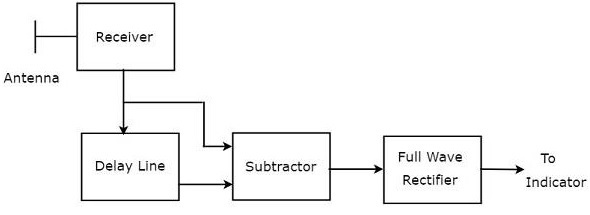
我们可以将多普勒效应后接收到的回波信号的数学方程写为 -

$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:方程\:1$$

在哪里，

A是视频信号的幅度

$f_d$ 是多普勒频率

$\phi_o$ 是相移，它等于 $4\pi f_tR_o/C$

通过将公式 1 中的 $t$ 替换为 $t-T_P$，我们将得到Delay line canceller 的输出。

$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:方程\:2$$

在哪里，

$T_P$ 是脉冲重复时间

我们通过从方程 1 中减去方程 2得到减法器输出。

$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2 }\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$

$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\ phi_0}{2} \右]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:方程\:3$$

减法器的输出用作全波整流器的输入。因此，全波整流器的输出如下图所示。它只不过是单个延迟线消除器的频率响应。

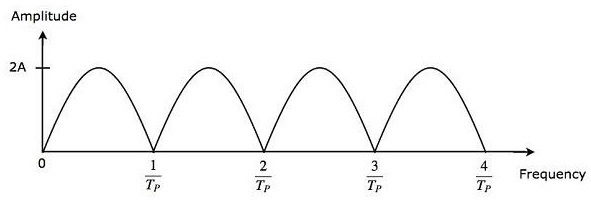
从公式 3 可以看出，当 $\pi f_dT_P$ 等于$\pi$的整数倍时，单延迟线消除器的频率响应变为零，这意味着 $\pi f_dT_P$ 等于 $n\ pi$ 从数学上来说，它可以写成

$$\pi f_dT_P=n\pi$$

$$\右箭头 f_dT_P=n$$

$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:方程\:4$$

从公式 4 中，我们可以得出结论，当多普勒频率 $f_d$ 等于脉冲重复时间 $T_P$ 的倒数整数倍时，单个延迟线消除器的频率响应变为零。

我们知道脉冲重复时间和脉冲重复频率之间存在以下关系。

$$f_d=\frac{1}{T_P}$$

$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:方程\:5$$

将公式 5 代入公式 4，我们将得到以下公式。

$$\Rightarrow f_d=nf_P\:\:\:\:\:方程\:6$$

从等式6中，我们可以得出结论，当多普勒频率$f_d$等于脉冲重复频率$f_P$的整数倍时，单个延迟线消除器的频率响应变为零。

盲目速度

根据我们目前了解到的情况，当 $n$ 等于 0 时，单个延迟线消除器消除了从静止目标接收到的回波信号的直流分量。除此之外，当多普勒频率 $f_d$ 等于脉冲重复频率$f_P$ 的整数倍（非零）时，它还消除了从非静止目标接收到的回波信号的交流分量。

因此，单个延迟线消除器的频率响应变为零的相对速度称为盲速度。从数学上来说，我们可以将盲速 $v_n$ 的表达式写为 -

$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:方程\:7$$

$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:方程\:8$$

在哪里，

$n$ 是一个整数，它等于 1、2、3 等

$\lambda$ 是工作波长

示例问题

MTI 雷达的工作频率为 6GHZ$，脉冲重复频率为 1KHZ$。找出该雷达的第一、第二和第三盲速。

解决方案

鉴于，

MTI雷达的工作频率，$f=6GHZ$

脉冲重复频率，$f_P=1KHZ$。

以下是用工作频率 f 表示的工作波长$\lambda$的公式。

$$\lambda=\frac{C}{f}$$

将 $C=3\times10^8m/sec$ 和 $f=6GHZ$ 代入上式中。

$$\lambda=\frac{3\times10^8}{6\times10^9}$$

$$\右箭头\lambda=0.05m$$

因此，当工作频率f为$6GHZ$时，工作波长$\lambda$等于$0.05m$。

我们知道以下盲速公式。

$$v_n=\frac{n\lambda f_p}{2}$$

通过将 $n$=1,2 & 3 代入上述方程，我们将分别得到第一、第二和第三盲速的以下方程。

$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$

$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$

$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$

将 $\lambda$ 和 $f_P$ 的值代入第一盲速方程中。

$$v_1=\frac{0.05\times 10^3}{2}$$

$$\右箭头 v_1=25m/sec$$

因此，对于给定的规格，第一盲速$v_1$ 等于 $25m/sec$。

通过代入以下值，我们将得到第二和第三盲速的值分别为 $50m/sec$ 和 $75m/sec$