数字电路 - 多路复用器
多路复用器是一个组合电路,最多具有 2 n 个数据输入、“n”条选择线和单输出线。这些数据输入之一将根据选择线的值连接到输出。
由于有“n”条选择线,因此将有 2 n种可能的 0 和 1 组合。因此,每种组合只会选择一个数据输入。多路复用器也称为Mux。
4x1 多路复用器
4x1 多路复用器有四个数据输入 I 3、 I 2、 I 1和 I 0,两条选择线 s 1和 s 0以及一个输出 Y。 4x1 多路复用器的框图如下图所示。
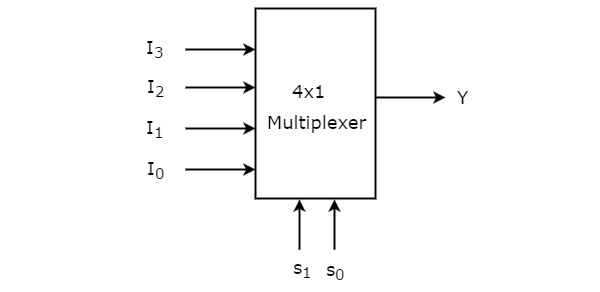
这 4 个输入之一将根据这两条选择线上存在的输入组合连接到输出。4x1 多路复用器的真值表如下所示。
| 选择线 | 输出 | |
|---|---|---|
| S 1 | 0 _ | 是 |
| 0 | 0 | 我0 |
| 0 | 1 | 我1 |
| 1 | 0 | 我2 |
| 1 | 1 | 我3 |
从真值表中,我们可以直接编写输出的布尔函数,Y为
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}' I_{2}+S_{1}S_{0}I_{3}$$
我们可以使用反相器、与门和或门来实现这个布尔函数。4x1多路复用器的电路图如下图所示。
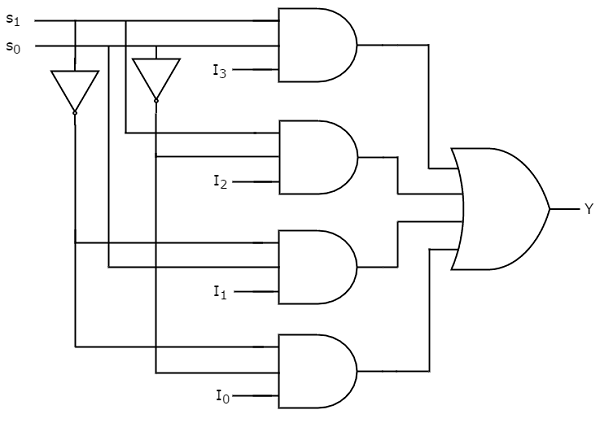
我们很容易理解上述电路的工作原理。同样,您可以按照相同的过程实现 8x1 多路复用器和 16x1 多路复用器。
高阶多路复用器的实现。
现在,让我们使用低阶多路复用器来实现以下两个高阶多路复用器。
- 8x1 多路复用器
- 16x1 多路复用器
8x1 多路复用器
在本节中,让我们使用 4x1 多路复用器和 2x1 多路复用器来实现 8x1 多路复用器。我们知道 4x1 多路复用器有 4 个数据输入、2 个选择线和 1 个输出。而 8x1 多路复用器有 8 个数据输入、3 个选择线和 1 个输出。
因此,我们在第一阶段需要两个4x1 多路复用器才能获得 8 个数据输入。由于每个 4x1 多路复用器产生一个输出,因此我们在第二级需要一个2x1 多路复用器,将第一级的输出视为输入并产生最终输出。
令8x1 多路复用器具有八个数据输入I 7至I 0、三条选择线s 2、s 1 & s0 以及一个输出Y。8x1 多路复用器的真值表如下所示。
| 选择输入 | 输出 | ||
|---|---|---|---|
| S 2 | S 1 | 0 _ | 是 |
| 0 | 0 | 0 | 我0 |
| 0 | 0 | 1 | 我1 |
| 0 | 1 | 0 | 我2 |
| 0 | 1 | 1 | 我3 |
| 1 | 0 | 0 | 我4 |
| 1 | 0 | 1 | 我5 |
| 1 | 1 | 0 | 我6 |
| 1 | 1 | 1 | 我7 |
通过考虑上面的真值表,我们可以使用低阶多路复用器轻松实现 8x1 多路复用器。8x1 多路复用器的框图如下图所示。
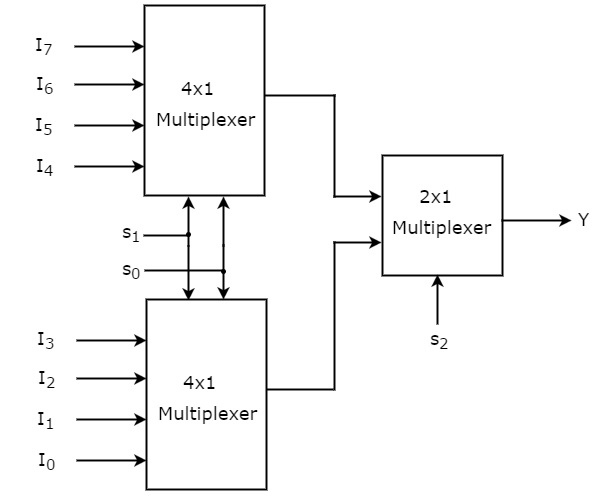
相同的选择线 s 1和 s 0应用于两个 4x1 多路复用器。上部4x1多路复用器的数据输入是I 7至I 4,下部4x1多路复用器的数据输入是I 3至I 0。因此,每个 4x1 多路复用器都会根据选择线 s 1和 s 0的值产生输出。
第一级 4x1 多路复用器的输出用作第二级中存在的 2x1 多路复用器的输入。另一条选择线 s 2应用于 2x1 多路复用器。
如果s 2为零,则2x1多路复用器的输出将是基于选择线s 1和s 0的值的4个输入I 3至I 0之一。
如果s 2为1,则2x1多路复用器的输出将是基于选择线s 1和s 0的值的4个输入I 7至I 4之一。
因此,两个 4x1 多路复用器和一个 2x1 多路复用器的整体组合相当于一个 8x1 多路复用器。
16x1 多路复用器
在本节中,让我们使用 8x1 多路复用器和 2x1 多路复用器来实现 16x1 多路复用器。我们知道8x1多路复用器有8个数据输入、3个选择线和1个输出。而 16x1 多路复用器有 16 个数据输入、4 个选择线和 1 个输出。
因此,我们在第一阶段需要两个8x1 多路复用器才能获得 16 个数据输入。由于每个 8x1 多路复用器产生一个输出,因此我们在第二级需要一个 2x1 多路复用器,将第一级的输出视为输入并产生最终输出。
设16x1多路复用器具有16个数据输入I 15至I 0、4条选择线s 3至s 0以及1个输出Y。16x1多路复用器的真值表如下所示。
| 选择输入 | 输出 | |||
|---|---|---|---|---|
| S 3 | S 2 | S 1 | 0 _ | 是 |
| 0 | 0 | 0 | 0 | 我0 |
| 0 | 0 | 0 | 1 | 我1 |
| 0 | 0 | 1 | 0 | 我2 |
| 0 | 0 | 1 | 1 | 我3 |
| 0 | 1 | 0 | 0 | 我4 |
| 0 | 1 | 0 | 1 | 我5 |
| 0 | 1 | 1 | 0 | 我6 |
| 0 | 1 | 1 | 1 | 我7 |
| 1 | 0 | 0 | 0 | 我8 |
| 1 | 0 | 0 | 1 | 我9 |
| 1 | 0 | 1 | 0 | 我10 |
| 1 | 0 | 1 | 1 | 我11 |
| 1 | 1 | 0 | 0 | 我12 |
| 1 | 1 | 0 | 1 | 我13 |
| 1 | 1 | 1 | 0 | 我14 |
| 1 | 1 | 1 | 1 | 我15 |
通过考虑上面的真值表,我们可以使用低阶多路复用器轻松实现 16x1 多路复用器。16x1 多路复用器的框图如下图所示。
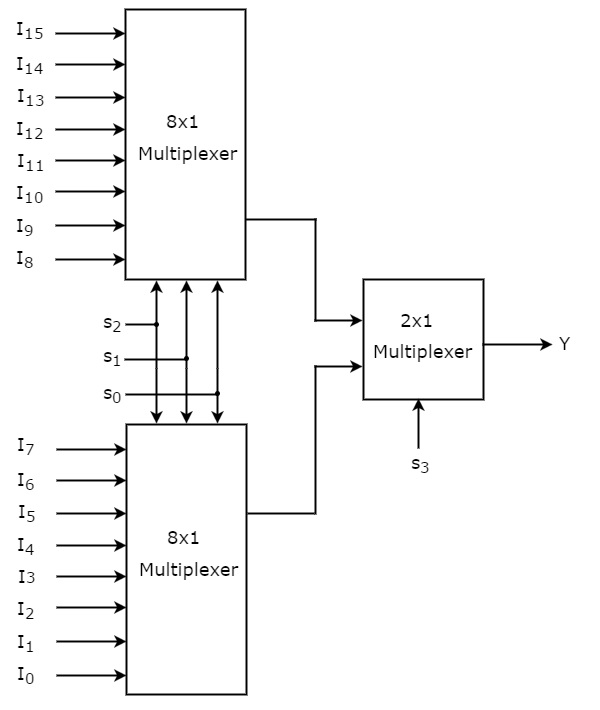
相同的选择线 s 2、s 1和 s 0应用于两个 8x1 多路复用器。上部8x1 多路复用器的数据输入是I 15至I 8,下部8x1 多路复用器的数据输入是I 7至I 0。因此,每个 8x1 多路复用器都会根据选择线 s 2、 s 1和 s 0的值产生输出。
第一级 8x1 多路复用器的输出用作第二级中存在的 2x1 多路复用器的输入。另一条选择线 s 3应用于 2x1 多路复用器。
如果s 3为零,则2x1多路复用器的输出将是基于选择线s 2、s 1和s 0的值的8个输入Is 7至I 0之一。
如果s 3为1,则2x1多路复用器的输出将是基于选择线s 2、s 1和s 0的值的8个输入I 15至I 8之一。
因此,两个 8x1 多路复用器和一个 2x1 多路复用器的总体组合相当于一个 16x1 多路复用器。
