数据结构-深度优先遍历

深度优先搜索 (DFS) 算法以深度运动方式遍历图，并在任何迭代中出现死胡同时，使用堆栈来记住获取下一个顶点以开始搜索。

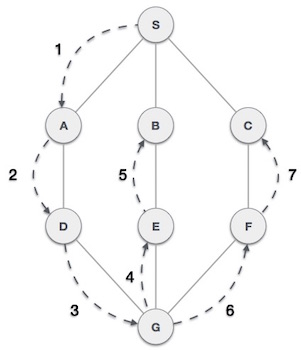
如上面给出的示例，DFS 算法首先从 S 遍历到 A、D、G、E、B，然后遍历到 F，最后遍历到 C。它采用以下规则。

规则 1 - 访问相邻的未访问顶点。将其标记为已访问。显示它。将其推入堆栈。
规则 2 - 如果未找到相邻顶点，则从堆栈中弹出一个顶点。（它会从堆栈中弹出所有没有相邻顶点的顶点。）
规则 3 - 重复规则 1 和规则 2，直到堆栈为空。

步	遍历	描述
1		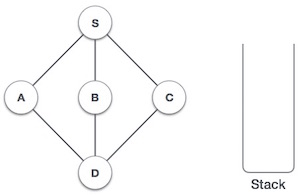初始化堆栈。
2		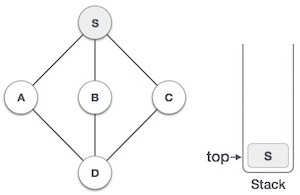将S标记为已访问并将其放入堆栈中。探索S中任何未访问过的相邻节点。我们有三个节点，我们可以选择其中任何一个。对于此示例，我们将按字母顺序获取节点。
3		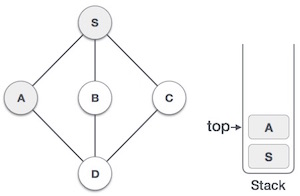将A标记为已访问并将其放入堆栈中。探索来自 A 的任何未访问的相邻节点。S和D都与A相邻，但我们只关心未访问的节点。
4		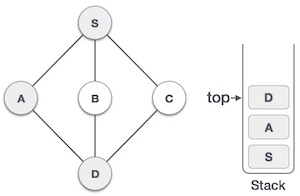访问D并将其标记为已访问并放入堆栈中。这里，我们有B和C节点，它们与D相邻，并且都未被访问。然而，我们将再次按字母顺序进行选择。
5		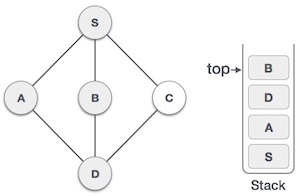我们选择B，将其标记为已访问并放入堆栈中。这里B没有任何未访问的相邻节点。所以，我们从堆栈中弹出B。
6		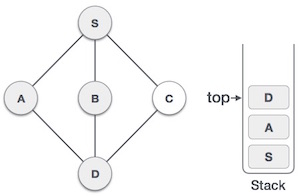我们检查栈顶是否返回到前一个节点，并检查是否有未访问的节点。在这里，我们发现D位于堆栈顶部。
7		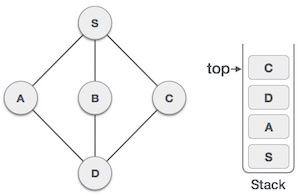现在来自D 的唯一未访问的相邻节点是C。因此，我们访问C，将其标记为已访问并将其放入堆栈中。

由于C没有任何未访问的相邻节点，因此我们不断弹出堆栈，直到找到具有未访问的相邻节点的节点。在这种情况下，没有任何内容，我们会继续弹出，直到堆栈为空。

例子

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
   char label;
   bool visited;
};
//stack variables
int stack[MAX]; 
int top = -1; 
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) { 
   stack[++top] = item; 
} 
int pop() { 
   return stack[top--]; 
} 
int peek() {
   return stack[top];
}
bool isStackEmpty() {
   return top == -1;
}
//graph functions

//add vertex to the vertex list
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;
   for(i = 0; i < vertexCount; i++) {
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) {
         return i;
      }
   }
   return -1;
}
void depthFirstSearch() {
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   //display the vertex
   displayVertex(0);   
   //push vertex index in stack
   push(0);
   while(!isStackEmpty()) {
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      //no adjacent vertex found
      if(unvisitedVertex == -1) {
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i = 0;i < vertexCount;i++) {
      lstVertices[i]->visited = false;
   }        
}
int main() {
   int i, j;

   for(i = 0; i < MAX; i++) {   // set adjacency
      for(j = 0; j < MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;
   }
   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4
   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D
   printf("Depth First Search: ");
   depthFirstSearch(); 
   return 0;   
}

输出

Depth First Search: S A D B C

//C++ code for Depth First Traversal
#include <iostream>
#include <array>
#include <vector>
constexpr int MAX = 5;
struct Vertex {
   char label;
   bool visited;
};
//stack variables
std::array<int, MAX> stack;
int top = -1;
//graph variables
//array of vertices 
std::array<Vertex*, MAX> lstVertices;
//adjacency matrix
std::array<std::array<int, MAX>, MAX> adjMatrix;
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
   stack[++top] = item;
}
int pop() {
   return stack[top--];
}
int peek() {
   return stack[top];
}
bool isStackEmpty() {
   return top == -1;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
   Vertex* vertex = new Vertex;
   vertex->label = label;
   vertex->visited = false;
   lstVertices[vertexCount++] = vertex;
}

//add edge to edge array
void addEdge(int start, int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//display the vertex
void displayVertex(int vertexIndex) {
   std::cout << lstVertices[vertexIndex]->label << " ";
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   for (int i = 0; i < vertexCount; i++) {
      if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i]->visited) {
         return i;
      }
   }
   return -1;
}
//mark first node as visited
void depthFirstSearch() {
   lstVertices[0]->visited = true;
   //display the vertex
   displayVertex(0);
   //push vertex index in stack
   push(0);
   while (!isStackEmpty()) {
       //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      //no adjacent vertex found
      if (unvisitedVertex == -1) {
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag
   for (int i = 0; i < vertexCount; i++) {
      lstVertices[i]->visited = false;
   }
}
int main() {
   for (int i = 0; i < MAX; i++) {   //set adjacency
      for (int j = 0; j < MAX; j++) {    // matrix to 0
         adjMatrix[i][j] = 0;
      }
   }
   addVertex('S');
   addVertex('A');
   addVertex('B');
   addVertex('C');
   addVertex('D');
   addEdge(0, 1);
   addEdge(0, 2);
   addEdge(0, 3);
   addEdge(1, 4);
   addEdge(2, 4);
   addEdge(3, 4);
   std::cout << "Depth First Search: ";
   depthFirstSearch();
   return 0;
}

输出

Depth First Search: S A D B C

//Java program for Depth First Traversal
public class DepthFirstSearch {
    private static final int MAX = 5;
    private static class Vertex {
        char label;
        boolean visited;
    }
    private static int[] stack = new int[MAX];
    private static int top = -1;
    private static Vertex[] lstVertices = new Vertex[MAX];
    private static int[][] adjMatrix = new int[MAX][MAX];
    private static int vertexCount = 0;
    private static void push(int item) {
        stack[++top] = item;
    }
    private static int pop() {
        return stack[top--];
    }
    private static int peek() {
        return stack[top];
    }
    private static boolean isStackEmpty() {
        return top == -1;
    }
    private static void addVertex(char label) {
        Vertex vertex = new Vertex();
        vertex.label = label;
        vertex.visited = false;
        lstVertices[vertexCount++] = vertex;
    }
    private static void addEdge(int start, int end) {
        adjMatrix[start][end] = 1;
        adjMatrix[end][start] = 1;
    }
    private static void displayVertex(int vertexIndex) {
        System.out.print(lstVertices[vertexIndex].label + " ");
    }
    private static int getAdjUnvisitedVertex(int vertexIndex) {
        for (int i = 0; i < vertexCount; i++) {
            if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i].visited) {
                return i;
            }
        }
        return -1;
    }
    private static void depthFirstSearch() {
        lstVertices[0].visited = true;
        displayVertex(0);
        push(0);
        while (!isStackEmpty()) {
            int unvisitedVertex = getAdjUnvisitedVertex(peek());

            if (unvisitedVertex == -1) {
                pop();
            } else {
                lstVertices[unvisitedVertex].visited = true;
                displayVertex(unvisitedVertex);
                push(unvisitedVertex);
            }
        }
        for (int i = 0; i < vertexCount; i++) {
            lstVertices[i].visited = false;
        }
    }
    public static void main(String[] args) {
        for (int i = 0; i < MAX; i++) {
            for (int j = 0; j < MAX; j++) {
                adjMatrix[i][j] = 0;
            }
        }
        addVertex('S');   // 0
        addVertex('A');   // 1
        addVertex('B');   // 2
        addVertex('C');   // 3
        addVertex('D');   // 4
        addEdge(0, 1);    // S - A
        addEdge(0, 2);    // S - B
        addEdge(0, 3);    // S - C
        addEdge(1, 4);    // A - D
        addEdge(2, 4);    // B - D
        addEdge(3, 4);    // C - D
        System.out.print("Depth First Search: ");
        depthFirstSearch();
    }
}

输出

Depth First Search: S A D B C

#Python program for Depth First Traversal
MAX = 5
class Vertex:
    def __init__(self, label):
        self.label = label
        self.visited = False
#stack variables
stack = []
top = -1
#graph variables
#array of vertices
lstVertices = [None] * MAX
#adjacency matrix
adjMatrix = [[0] * MAX for _ in range(MAX)]
#vertex count
vertexCount = 0
#stack functions
def push(item):
    global top
    top += 1
    stack.append(item)
def pop():
    global top
    item = stack[top]
    del stack[top]
    top -= 1
    return item
def peek():
    return stack[top]
def isStackEmpty():
    return top == -1
#graph functions
#add vertex to the vertex list
def addVertex(label):
    global vertexCount
    vertex = Vertex(label)
    lstVertices[vertexCount] = vertex
    vertexCount += 1
#add edge to edge array
def addEdge(start, end):
    adjMatrix[start][end] = 1
    adjMatrix[end][start] = 1
#Display the Vertex
def displayVertex(vertexIndex):
    print(lstVertices[vertexIndex].label, end=' ')
def getAdjUnvisitedVertex(vertexIndex):
    for i in range(vertexCount):
        if adjMatrix[vertexIndex][i] == 1 and not lstVertices[i].visited:
            return i
    return -1
def depthFirstSearch():
    lstVertices[0].visited = True
    displayVertex(0)
    push(0)
    while not isStackEmpty():
        unvisitedVertex = getAdjUnvisitedVertex(peek())
        if unvisitedVertex == -1:
            pop()
        else:
            lstVertices[unvisitedVertex].visited = True
            displayVertex(unvisitedVertex)
            push(unvisitedVertex)
    for i in range(vertexCount):
        lstVertices[i].visited = False
for i in range(MAX):
    for j in range(MAX):
        adjMatrix[i][j] = 0
addVertex('S')   # 0
addVertex('A')   # 1
addVertex('B')   # 2
addVertex('C')   # 3
addVertex('D')   # 4
addEdge(0, 1)    # S - A
addEdge(0, 2)    # S - B
addEdge(0, 3)    # S - C
addEdge(1, 4)    # A - D
addEdge(2, 4)    # B - D
addEdge(3, 4)    # C - D
print("Depth First Search:", end=' ')
depthFirstSearch()

输出

Depth First Search: S A D B C