计算机图形学 - 快速指南

计算机图形学 - 基础知识

计算机图形学是一门借助编程在计算机屏幕上绘制图片的艺术。它涉及数据的计算、创建和操作。换句话说，我们可以说计算机图形学是一种用于生成和操作图像的渲染工具。

阴极射线管

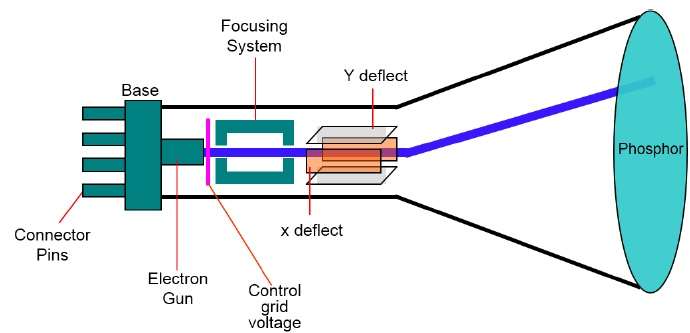
图形系统中的主要输出设备是视频监视器。视频监视器的主要元件是阴极射线管 (CRT)，如下图所示。

CRT 的操作非常简单 -

电子枪发射电子束（阴极射线）。
电子束穿过聚焦和偏转系统，将其引导至涂有荧光粉的屏幕上的指定位置。
当电子束击中屏幕时，荧光粉在电子束接触的每个位置处发出一个小光点。
它通过将电子束快速引导回相同的屏幕点来重新绘制图像。

我们可以通过两种方式（随机扫描和光栅扫描）在屏幕上显示对象。

光栅扫描

在光栅扫描系统中，电子束从上到下扫过屏幕，一次一行。当电子束穿过每一行时，电子束强度会打开和关闭，以创建照明点图案。

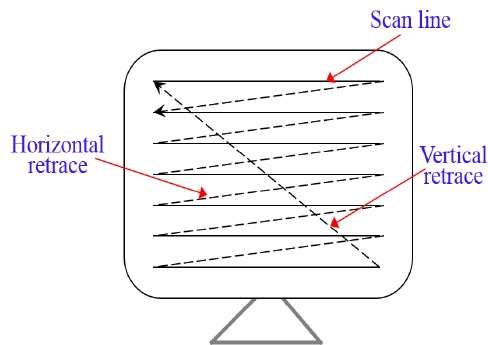
图片定义存储在称为刷新缓冲区或帧缓冲区的内存区域中。该存储区域保存所有屏幕点的强度值集。然后从刷新缓冲区检索存储的强度值，并一次一行（扫描线）“绘制”在屏幕上，如下图所示。

每个屏幕点称为像素（图片元素）或pel。在每条扫描线结束时，电子束返回到屏幕左侧以开始显示下一条扫描线。

随机扫描（矢量扫描）

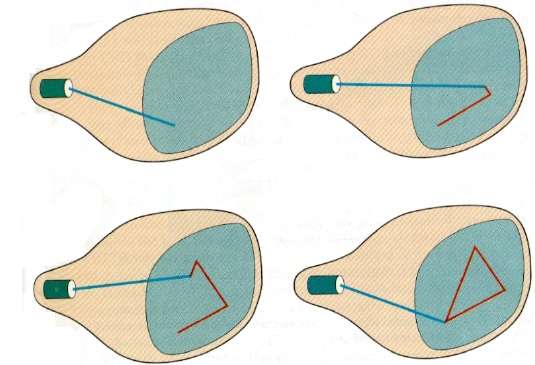
在这种技术中，电子束仅定向到屏幕上要绘制图像的部分，而不是像光栅扫描那样从左到右、从上到下扫描。也称为矢量显示、笔画显示、书法显示。

图片定义作为一组画线命令存储在称为刷新显示文件的内存区域中。为了显示指定的图片，系统循环显示文件中的命令集，依次绘制每个组件线。处理完所有画线命令后，系统循环回到列表中的第一条画线命令。

随机扫描显示器设计为每秒绘制图片的所有组成线 30 到 60 次。

计算机图形学应用

计算机图形学有许多应用，其中一些应用如下 -

计算机图形用户界面（GUI） - 一种图形、面向鼠标的范例，允许用户与计算机交互。
商业演示图形- “一图胜千言”。
制图学- 绘制地图。
天气地图- 实时地图、符号表示。
卫星成像- 测地线图像。
照片增强- 锐化模糊的照片。
医学成像- MRI、CAT 扫描等 - 非侵入性内部检查。
工程图纸- 机械、电气、土木等 - 取代过去的蓝图。
版式- 在出版中使用字符图像 - 取代过去的硬类型。
建筑- 施工计划、外部草图 - 取代过去的蓝图和手绘图。
艺术- 计算机为艺术家提供了一种新的媒介。
培训- 飞行模拟器、计算机辅助教学等。
娱乐- 电影和游戏。
模拟和建模- 取代物理建模和制定

线生成算法

一条线连接两点。它是图形中的基本元素。要绘制一条线，您需要可以在两个点之间绘制一条线。在以下三种算法中，我们将直线上的一个点称为$X_{0}，Y_{0}$，将直线上的第二个点称为$X_{1}，Y_{1}$。

DDA算法

数字差分分析器 (DDA) 算法是简单的线生成算法，此处将逐步说明。

步骤 1 - 获取两个端点 $(X_{0}, Y_{0})$ 和 $(X_{1}, Y_{1})$ 的输入。

步骤 2 - 计算两个端点之间的差异。

dx = X₁ - X₀
dy = Y₁ - Y₀

步骤 3 - 根据步骤 2 中计算出的差异，您需要确定放置像素的步骤数。如果 dx > dy，则 x 坐标需要更多步骤；否则在 y 坐标中。

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

步骤 4 - 计算 x 坐标和 y 坐标的增量。

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

步骤 5 - 通过成功地相应增加 x 和 y 坐标来放置像素并完成线条的绘制。

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

布雷森汉姆线一代

Bresenham算法是另一种增量扫描转换算法。该算法的一大优点是，它仅使用整数计算。以单位间隔跨 x 轴移动，并在每一步在两个不同的 y 坐标之间进行选择。

例如，如下图所示，从位置 (2, 3) 开始，您需要在 (3, 3) 和 (3, 4) 之间进行选择。您想要更接近原始线的点。

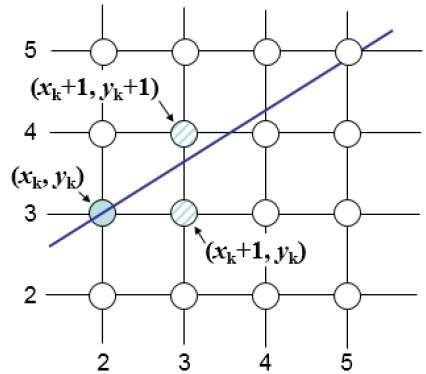
在样本位置 $X_{k}+1,$ 处，与数学线的垂直间距标记为 $d_{upper}$ 和 $d_{lower}$。

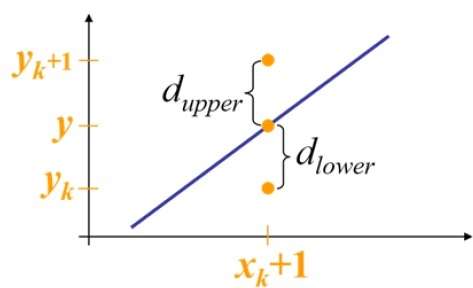
从上图中，$x_{k}+1$ 处数学直线上的 y 坐标为 -

Y = m($X_{k}$+1) + b

因此，$d_{upper}$ 和 $d_{lower}$ 给出如下 -

$$d_{下} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

和

$$d_{上} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

您可以使用它们来简单地决定哪个像素更接近数学线。这个简单的决定是基于两个像素位置之间的差异。

$$d_{下} - d_{上} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

让我们用dy/dx代替m，其中dx和dy是端点之间的差值。

$$dx (d_{下} - d_{上}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

因此，一条线上第k步的决策参数 $P_{k}$由下式给出 -

$$p_{k} = dx(d_{下} - d_{上})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

决策参数$P_{k}$的符号与$d_{lower} - d_{upper}$的符号相同。

如果$p_{k}$为负，则选择下方的像素，否则选择上方的像素。

请记住，坐标变化沿 x 轴以单位步长发生，因此您可以通过整数计算完成所有操作。在步骤 k+1，决策参数给出为 -

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

从中减去 $p_{k}$ 我们得到 -

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

但是，$x_{k+1}$ 与 $x_{k+1}$ 相同。所以 -

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

其中，$Y_{k+1} – Y_{k}$ 为 0 或 1，具体取决于 $P_{k}$ 的符号。

第一个决策参数 $p_{0}$ 在 $(x_{0}, y_{0})$ 处计算，计算公式为 -

$$p_{0} = 2dy - dx$$

现在，记住上述所有要点和计算，这是斜率 m < 1 的 Bresenham 算法 -

步骤 1 - 输入线的两个端点，将左端点存储在 $(x_{0}, y_{0})$ 中。

步骤 2 - 绘制点 $(x_{0}, y_{0})$。

步骤 3 - 计算常数 dx、dy、2dy 和 (2dy – 2dx) 并获得决策参数的第一个值：

$$p_{0} = 2dy - dx$$

步骤 4 - 在沿线的每个 $X_{k}$ 处，从 k = 0 开始，执行以下测试 -

如果 $p_{k}$ < 0，则下一个要绘制的点是 $(x_{k}+1, y_{k})$ 并且

$$p_{k+1} = p_{k} + 2dy$$ 否则，

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

步骤 5 - 重复步骤 4 (dx – 1) 次。

当 m > 1 时，确定每次增加 y 的同时是否需要增加 x。

求解后，决策参数 $P_{k}$ 的方程将非常相似，只是方程中的 x 和 y 互换。

中点算法

中点算法源自 Bresenham，并由 Pitteway 和 Van Aken 修改。假设您已将点 P 放置在 (x, y) 坐标处，并且直线的斜率为 0 ≤ k ≤ 1，如下图所示。

现在您需要决定是否将下一个点放在 E 或 N 处。这可以通过识别最接近点 N 或 E 的交点 Q 来选择。如果交点 Q 最接近点 N，则 N 被视为下一点；否则E。

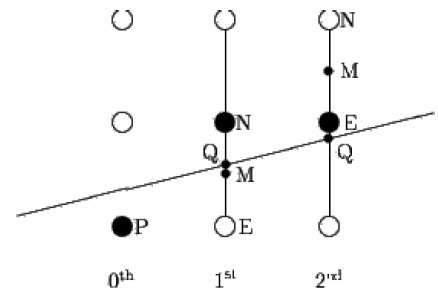
为了确定这一点，首先计算中点 M(x+1, y + ½)。如果E和N的垂线的交点Q在M的下方，则取E作为下一个点；否则取N作为下一个点。

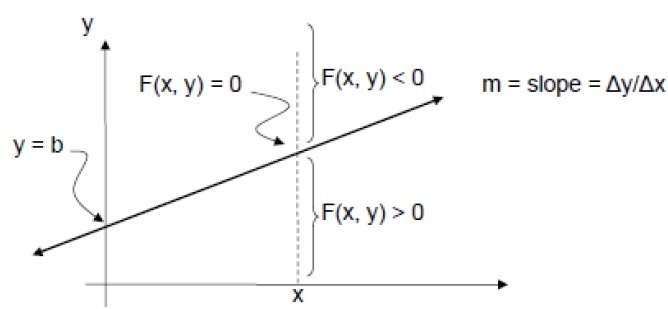
为了检查这一点，我们需要考虑隐式方程 -

F(x,y) = mx + b - y

对于任何给定 X 处的正 m，

如果 y 在线，则 F(x, y) = 0
如果 y 在线上方，则 F(x, y) < 0
如果 y 在线下方，则 F(x, y) > 0

圆生成算法

在屏幕上画一个圆比画一条线稍微复杂一些。有两种流行的生成圆的算法 - Bresenham 算法和中点圆算法。这些算法基于确定绘制圆所需的后续点的思想。让我们详细讨论算法 -

圆的方程为 $X^{2} + Y^{2} = r^{2},$ 其中 r 是半径。

布雷森纳姆算法

我们无法在光栅显示器上显示连续的弧线。相反，我们必须选择最近的像素位置来完成弧线。

从下图中，您可以看到我们已将像素放置在 (X, Y) 位置，现在需要决定将下一个像素放置在何处 - 在 N (X+1, Y) 或 S (X+1, Y-1）。

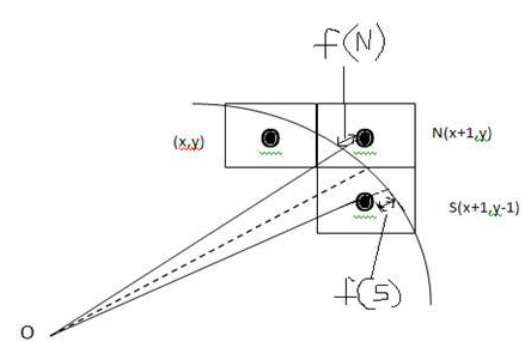
这可以由决策参数d来决定。

如果 d <= 0，则选择 N(X+1, Y) 作为下一个像素。
如果 d > 0，则选择 S(X+1，Y-1) 作为下一个像素。

算法

步骤 1 - 获取圆心和半径的坐标，并将它们分别存储在 x、y 和 R 中。设置 P=0 且 Q=R。

步骤 2 - 设置决策参数 D = 3 – 2R。

步骤 3 - 当 P ≤ Q 时重复步骤 8。

步骤 4 - 调用画圆 (X, Y, P, Q)。

步骤 5 - 增加 P 的值。

步骤 6 - 如果 D < 0，则 D = D + 4P + 6。

步骤 7 - 否则设置 R = R - 1, D = D + 4(PQ) + 10。

步骤 8 - 调用画圆 (X, Y, P, Q)。

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

中点算法

步骤 1 - 输入半径r和圆心 $(x_{c,} y_{c})$ 并获得以原点为中心的圆圆周上的第一个点：

(x₀, y₀) = (0, r)

步骤 2 - 计算决策参数的初始值：

$P_{0}$ = 5/4 – r（有关该方程的简化，请参阅以下说明。）

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0

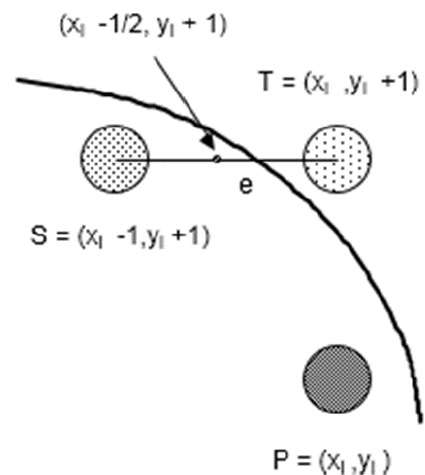
Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

步骤 3 - 在从 K=0 开始的每个 $X_{K}$ 位置，执行以下测试 -

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

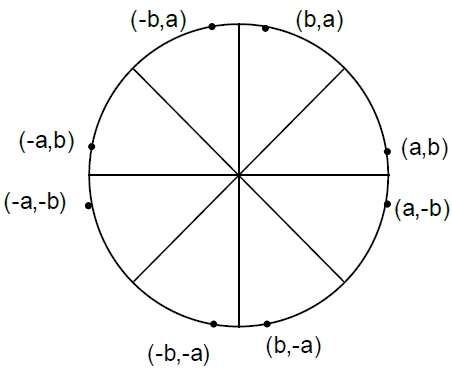
步骤 4 - 确定其他七个八分圆中的对称点。

步骤 5 - 将每个计算像素位置 (X, Y) 移动到以 $(X_{C,} Y_{C})$ 为中心的圆形路径上并绘制坐标值。

X = X + X_C,   Y = Y + Y_C

步骤 6 - 重复步骤 3 到 5，直到 X >= Y。

多边形填充算法

多边形是顶点的有序列表，如下图所示。为了用特定的颜色填充多边形，您需要确定落在多边形边界上的像素和落在多边形内部的像素。在本章中，我们将了解如何使用不同的技术填充多边形。

扫描线算法

该算法的工作原理是使扫描线与多边形边相交，并填充交点对之间的多边形。以下步骤描述了该算法的工作原理。

步骤 1 - 找出给定多边形的 Ymin 和 Ymax。

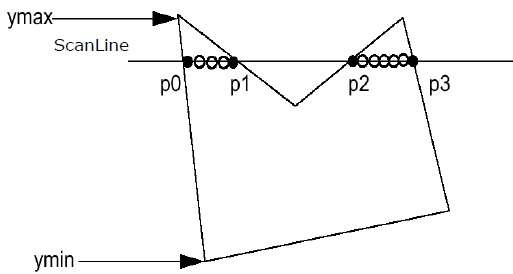
步骤 2 - 扫描线与多边形的每条边从 Ymin 到 Ymax 相交。命名多边形的每个交点。如上图所示，它们被命名为p0、p1、p2、p3。

步骤 3 - 按 X 坐标的升序对交点进行排序，即 (p0, p1)、(p1, p2) 和 (p2, p3)。

步骤 4 - 填充多边形内的所有坐标对并忽略备用对。

洪水填充算法

有时我们会遇到一个对象，我们想要用不同的颜色填充该区域及其边界。我们可以使用指定的内部颜色绘制此类对象，而不是像边界填充算法中那样搜索特定的边界颜色。

它不依赖于对象的边界，而是依赖于填充颜色。换句话说，它用填充颜色替换对象的内部颜色。当不再存在原始内部颜色的像素时，算法完成。

该算法再次依赖于填充像素的四连接或八连接方法。但它不是寻找边界颜色，而是寻找属于内部的所有相邻像素。

边界填充算法

边界填充算法顾名思义。该算法在对象内部选取一个点并开始填充，直到它到达对象的边界。为了使该算法发挥作用，边界的颜色和我们填充的颜色应该不同。

在此算法中，我们假设整个对象的边界颜色相同。边界填充算法可以通过4连接像素或8连接像素来实现。

四连通多边形

在此技术中，使用 4 个连接的像素，如图所示。我们将像素放置在当前像素的上方、下方、右侧和左侧，并且此过程将继续，直到找到具有不同颜色的边界。

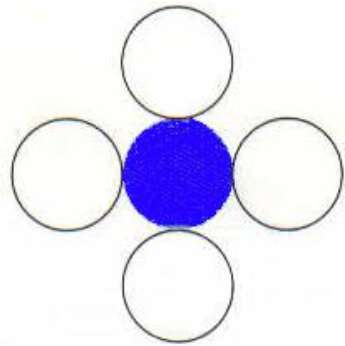
算法

步骤 1 - 初始化种子点（seedx、seedy）、fcolor 和 dcol 的值。

步骤 2 - 定义多边形的边界值。

步骤 3 - 检查当前种子点是否为默认颜色，然后重复步骤 4 和 5 直到到达边界像素。

If getpixel(x, y) = dcol then repeat step 4 and 5

步骤 4 - 使用种子点的填充颜色更改默认颜色。

setPixel(seedx, seedy, fcol)

步骤 5 - 递归地遵循四个邻域点的过程。

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

第 6 步- 退出

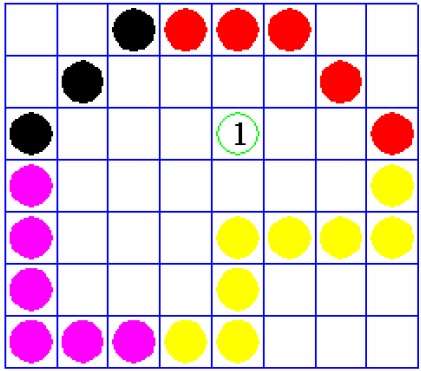
这种技术有一个问题。考虑如下所示的情况，我们尝试填充整个区域。此处，图像仅被部分填充。在这种情况下，不能使用4连接像素技术。

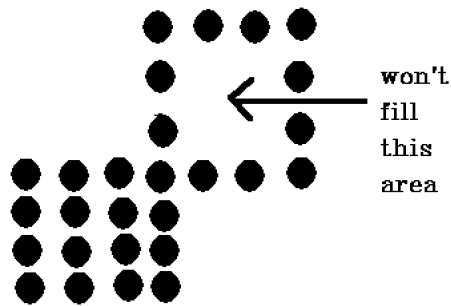
8连通多边形

在此技术中，使用 8 个连接的像素，如图所示。我们将像素放置在当前像素的上方、下方、右侧和左侧，就像我们在 4 连接技术中所做的那样。

除此之外，我们还将像素放在对角线上，以便覆盖当前像素的整个区域。这个过程将继续，直到我们找到不同颜色的边界。

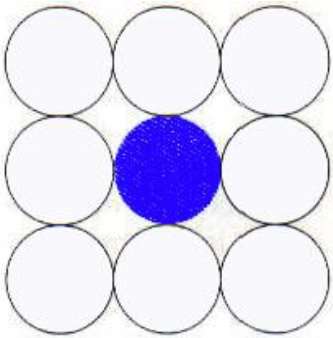
算法

步骤 1 - 初始化种子点（seedx、seedy）、fcolor 和 dcol 的值。

步骤 2 - 定义多边形的边界值。

步骤 3 - 检查当前种子点是否为默认颜色，然后重复步骤 4 和 5 直到达到边界像素

If getpixel(x,y) = dcol then repeat step 4 and 5

步骤 4 - 使用种子点的填充颜色更改默认颜色。

setPixel(seedx, seedy, fcol)

步骤 5 - 递归地遵循四个邻域点的过程

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

第 6 步- 退出

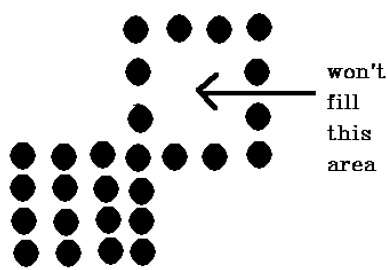
4 连接像素技术无法填充下图标记的区域，而 8 连接技术不会发生这种情况。

内外测试

这种方法也称为计数法。在填充对象时，我们经常需要识别特定点是在对象内部还是外部。有两种方法可以识别特定点是在物体内部还是外部。

奇偶规则
非零绕数规则

奇偶规则

在这种技术中，我们计算沿线从任意点 (x, y) 到无穷远交叉的边。如果交互次数是奇数，则点 (x, y) 是内点。如果交互次数是偶数，则点 (x, y) 是外部点。这是一个例子，可以让您清楚地了解 -

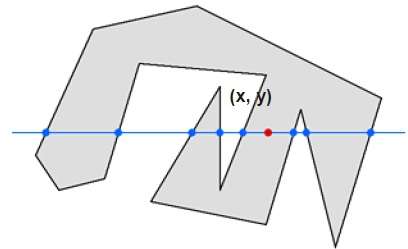
从上图可以看出，从点(x,y)开始，左边的交互点数量为5个，右边的交互点数量为3个，所以交互点总数为8个，是奇数。因此，该点被认为是在对象内。

非零缠绕数规则

此方法也可与简单多边形一起使用来测试给定点是否在内部。借助大头针和橡皮筋就可以简单地理解它。将大头针固定在多边形的一条边上，并将橡皮筋绑在其中，然后沿着多边形的边拉伸橡皮筋。

当多边形的所有边都被橡皮筋覆盖后，检查已固定在待测点处的销钉。如果我们在该点发现至少有一阵风，则认为它在多边形内，否则我们可以说该点不在多边形内。

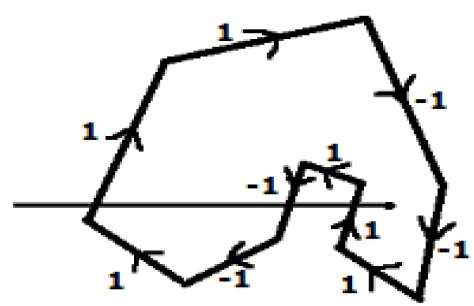
在另一种替代方法中，给出多边形所有边的方向。从待测点向X方向最左侧画一条扫描线。

将值 1 赋予所有向上方向的边，将所有其他边赋予 -1 作为方向值。
检查扫描线所经过的边缘方向值并将它们相加。
如果该方向值的总和不为零，则该待测点为内点，否则为外点。
上图中，我们将扫描线所经过的方向值相加，则总数为1 – 1 + 1 = 1；这是非零的。所以该点被称为内点。

查看和剪辑

计算机图形学中剪裁的主要用途是删除查看窗格之外的对象、线条或线段。观看变换对点相对于观看体积的位置不敏感——尤其是观看者后面的那些点——并且有必要在生成视图之前删除这些点。

点剪裁

从给定窗口剪切一个点非常容易。考虑下图，其中矩形表示窗口。点裁剪告诉我们给定点（X，Y）是否在给定窗口内；并决定是否使用窗口的最小和最大坐标。

如果 X 位于 Wx1 ≤ X ≤ Wx2 之间，则给定点的 X 坐标位于窗口内。同样，如果 Y 位于 Wy1 ≤ Y ≤ Wy2 之间，则给定点的 Y 坐标位于窗口内。

线裁剪

线裁剪的概念与点裁剪相同。在线条裁剪中，我们将剪切窗口外部的线条部分，仅保留窗口内部的部分。

科恩-萨瑟兰线剪报

该算法使用如下图所示的裁剪窗口。剪切区域的最小坐标为 $(XW_{min,} YW_{min})$，剪切区域的最大坐标为 $(XW_{max,} YW_{max})$。

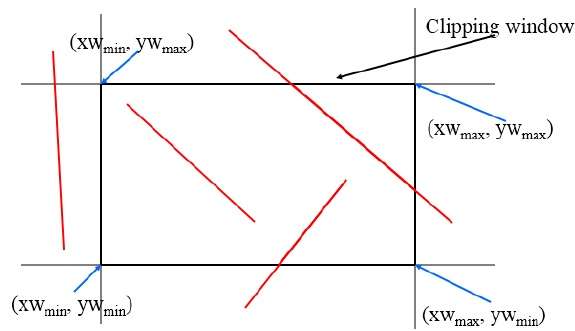
我们将使用 4 位来划分整个区域。这 4 位代表区域的顶部、底部、右侧和左侧，如下图所示。这里，TOP和LEFT位被设置为 1，因为它是左上角。

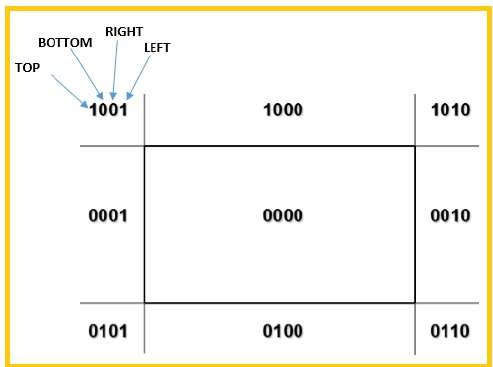
该行有 3 种可能性 -

线可以完全在窗口内（这条线应该被接受）。
线可以完全在窗口之外（这条线将被完全移出区域）。
线条可以部分位于窗口内部（我们将找到交点并仅绘制位于区域内部的那部分线条）。

算法

步骤 1 - 为每个端点分配区域代码。

步骤 2 - 如果两个端点的区域代码都是0000，则接受此行。

步骤 3 - 否则，对两个区域代码执行逻辑AND运算。

步骤 3.1 - 如果结果不是0000，则拒绝该行。

步骤 3.2 - 否则你需要剪辑。

步骤 3.2.1 - 选择窗口外线的端点。

步骤 3.2.2 - 找到窗口边界处的交点（基于区域代码）。

步骤 3.2.3 - 将端点替换为交点并更新区域代码。

步骤 3.2.4 - 重复步骤 2，直到我们找到一条被简单接受或简单拒绝的剪裁线。

步骤 4 - 对其他线路重复步骤 1。

Cyrus-Beck 线裁剪算法

该算法比 Cohen-Sutherland 算法更高效。它采用参数线表示和简单的点积。

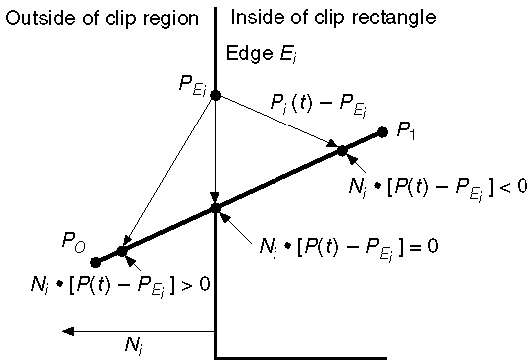
直线的参数方程为 -

P₀P₁:P(t) = P₀ + t(P₁-P₀)

令 N _i为向外法线边 E _i。现在选取边缘 E _i上的任意点 P _Ei，然后点积 N _i ∙[P(t) – P _Ei ] 确定点 P(t) 是“剪辑边缘内部”还是“剪辑边缘外部”或剪辑边缘“上”。

_{如果 N i} .[P(t) – P _Ei ] < 0，则点 P(t) 位于内部

_{如果 N i} .[P(t) – P _Ei ] > 0，则点 P(t) 位于外部

_如果Ni .[P(t) – P _Ei ] = 0（交点），则点 P(t) 位于边缘上

Ni _. [P(t) – P _Ei ] = 0

Ni _. [ P ₀ + t(P ₁ -P ₀ ) – P _Ei ] = 0（将 P(t) 替换为 P ₀ + t(P ₁ -P ₀ )）

Ni _. [P ₀ – P _Ei ] + Ni _.t [P ₁ -P ₀ ] = 0

Ni _. [P ₀ – P _Ei ] + Ni _∙ tD = 0（用 D 代替 [P ₁ -P ₀ ]）

Ni _. [P ₀ – P _Ei ] = - Ni _∙ tD

t 的方程变为，

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

它在以下条件下有效 -

N _i ≠ 0（错误不会发生）
D ≠ 0 (P ₁ ≠ P ₀ )
Ni ∙D ≠ 0 (P _{0 P 1}_不平行_于E _i )

多边形裁剪（Sutherland Hodgman 算法）

还可以通过指定剪切窗口来剪切多边形。Sutherland Hodgeman多边形裁剪算法用于多边形裁剪。在此算法中，多边形的所有顶点都针对裁剪窗口的每条边进行裁剪。

首先，将多边形剪裁到多边形窗口的左边缘，以获得多边形的新顶点。这些新顶点用于根据剪切窗口的右边缘、顶部边缘、底部边缘来剪切多边形，如下图所示。

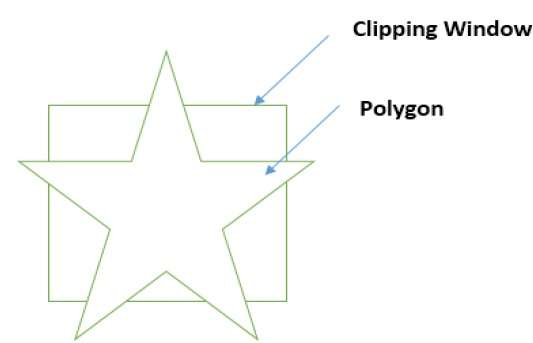
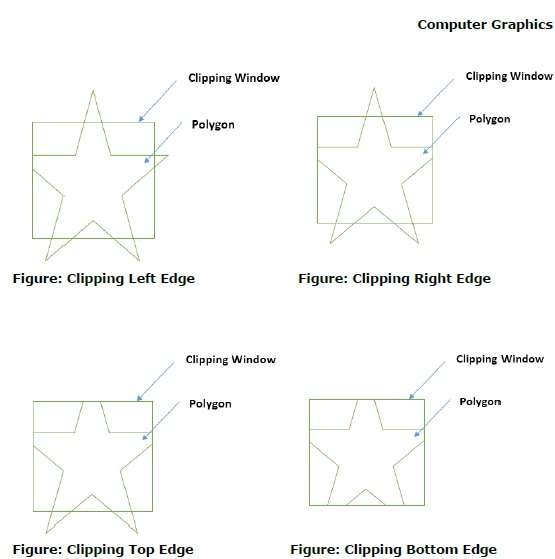
在用裁剪窗口处理多边形的边缘时，如果边缘不完全在裁剪窗口内，则找到交点，并剪掉从交点到外侧边缘的部分边缘。下图显示了左、右、上、下边缘剪裁 -

文本剪辑

使用各种技术来提供计算机图形中的文本剪辑。这取决于用于生成字符的方法和特定应用程序的要求。下面列出了三种文本剪辑方法 -

全部或无字符串剪辑
全部或无字符剪辑
文字剪裁

下图显示了全部或无字符串剪辑 -

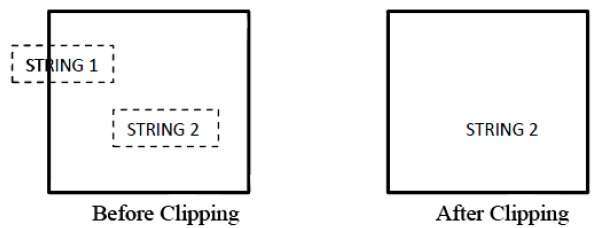
在全或无字符串剪切方法中，我们要么保留整个字符串，要么根据剪切窗口拒绝整个字符串。如上图所示，STRING2 完全位于剪切窗口内，因此我们保留它，而 STRING1 仅部分位于窗口内，我们拒绝。

下图显示了全部或无字符剪辑 -

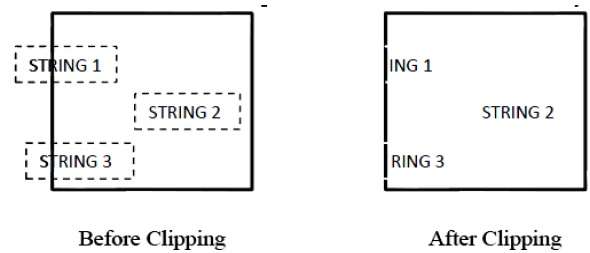
这种剪切方法基于字符而不是整个字符串。在此方法中，如果字符串完全位于剪切窗口内，则我们保留它。如果它部分位于窗外，则 -

您仅拒绝字符串外部的部分
如果字符位于剪切窗口的边界上，则我们丢弃整个字符并保留其余字符串。

下图显示了文本剪辑 -

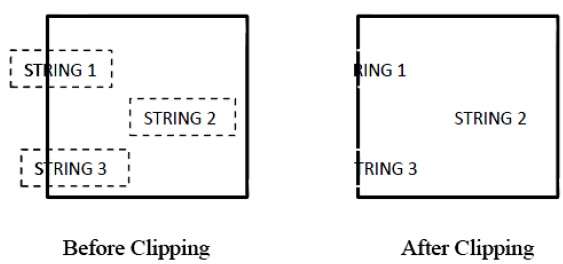
这种裁剪方法是基于字符而不是整个字符串。在此方法中，如果字符串完全位于剪切窗口内，则我们保留它。如果部分位于窗外，则

您仅拒绝字符串位于外部的部分。
如果字符位于剪切窗口的边界上，则我们仅丢弃位于剪切窗口之外的字符部分。

位图图形

位图是描述图像的像素的集合。它是计算机图形学的一种，计算机用来存储和显示图片。在这种类型的图形中，图像是一点一点地存储的，因此被称为位图图形。为了更好地理解，让我们考虑以下示例，其中我们使用位图图形绘制笑脸。

现在我们来看看这张笑脸是如何在计算机图形学中一点一点存储起来的。

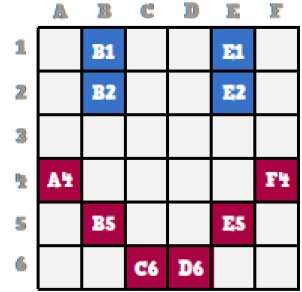
仔细观察原来的笑脸，我们可以看到有两条蓝色的线，分别表示为上图中的B1、B2和E1、E2。

同样，笑脸分别用A4、B5、C6、D6、E5和F4的组合位来表示。

位图图形的主要缺点是 -

我们无法调整位图图像的大小。如果您尝试调整大小，像素会变得模糊。
彩色位图可能非常大。

2D 变换

转换是指通过应用规则将某些图形变成其他图形。我们可以有各种类型的变换，例如平移、放大或缩小、旋转、剪切等。当变换发生在 2D 平面上时，称为 2D 变换。

变换在计算机图形学中发挥着重要作用，可以重新定位屏幕上的图形并更改其大小或方向。

齐次坐标

要执行一系列变换，例如平移、旋转和缩放，我们需要遵循一个顺序过程 -

平移坐标，
旋转平移后的坐标，然后
缩放旋转坐标以完成复合变换。

为了缩短这个过程，我们必须使用 3×3 变换矩阵来代替 2×2 变换矩阵。要将 2×2 矩阵转换为 3×3 矩阵，我们必须添加一个额外的虚拟坐标 W。

这样，我们就可以用3个数字而不是2个数字来表示该点，这称为齐次坐标系。在这个系统中，我们可以用矩阵乘法来表示所有的变换方程。_{任何笛卡尔点 P(X, Y) 都可以通过 P' (X h} , Y _h , h)转换为齐次坐标。

翻译

平移将对象移动到屏幕上的不同位置。_{您可以通过将平移坐标 (t x} , t _y ) 添加到原始坐标 (X, Y) 来获得新坐标 (X', Y')，从而平移 2D 中的点。

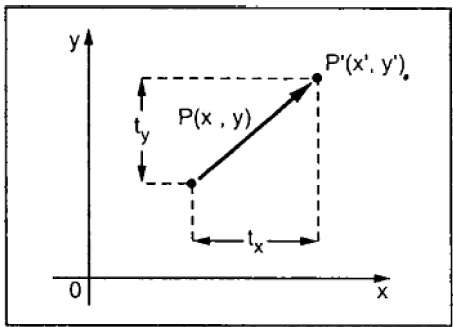
从上图中，你可以写出 -

X' = X + t _x

Y' = Y + _y

(t _x , t _y ) 对称为平移向量或平移向量。上述方程也可以使用列向量来表示。

$P = \frac{[X]}{[Y]}$ p' = $\frac{[X']}{[Y']}$ T = $\frac{[t_{x}]}{[ t_{y}]}$

我们可以将其写为 -

P' = P + T

回转

在旋转中，我们将物体从其原点旋转特定的角度 θ (theta)。从下图中我们可以看出，点 P(X, Y) 与水平 X 坐标的夹角为 φ，距原点的距离为 r。

假设您想将其旋转角度 θ。旋转到新位置后，您将得到一个新点P'（X'，Y'）。

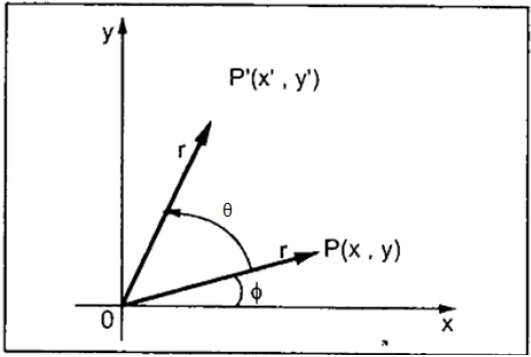
使用标准三角函数，点 P(X, Y) 的原始坐标可以表示为 -

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同样，我们可以将点 P' (X', Y') 表示为 -

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \ : sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \ : sin \: \phi \: cos \: \theta ....... (4)$

将式(1)、(2)分别代入(3)、(4)，可得

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

将上式表示为矩阵形式，

$$[X' Y'] = [XY] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P' = P ∙ R

其中 R 是旋转矩阵

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

旋转角度可正可负。

对于正旋转角度，我们可以使用上面的旋转矩阵。然而，对于负角度旋转，矩阵将发生如下变化 -

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

缩放

为了改变对象的大小，使用缩放变换。在缩放过程中，您可以扩大或压缩对象的尺寸。可以通过将对象的原始坐标乘以缩放因子来实现缩放，以获得所需的结果。

我们假设原始坐标为 (X, Y)，缩放因子为 (S _X , S _Y )，生成的坐标为 (X', Y')。这可以用数学方式表示，如下所示 -

X' = X 。S _X 和 Y' = Y 。SY _{_}

缩放因子S _X、S _Y分别在X和Y方向上缩放对象。上述方程也可以用矩阵形式表示如下 -

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

或者

P' = P 。S

其中 S 是缩放矩阵。缩放过程如下图所示。

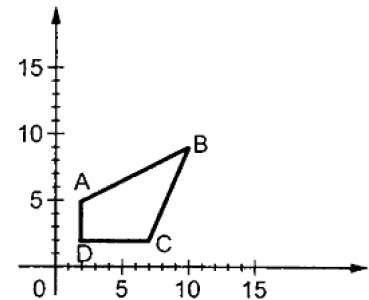
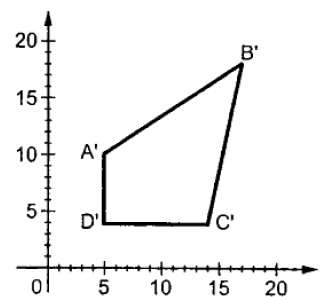
如果我们为缩放因子 S 提供小于 1 的值，那么我们可以减小对象的大小。如果我们提供大于 1 的值，那么我们可以增加对象的大小。

反射

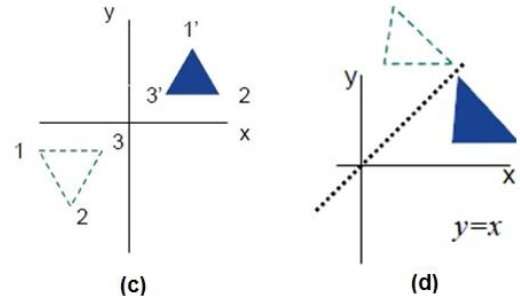
反射是原物体的镜像。换句话说，我们可以说这是一个180°的旋转操作。在反射变换中，物体的大小不会改变。

下图分别显示了相对于 X 轴和 Y 轴以及相对于原点的反射。

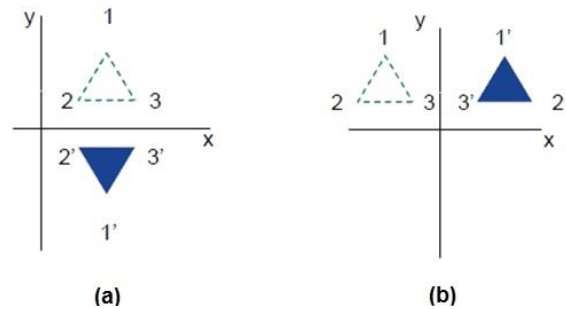
剪切

使物体形状倾斜的变换称为剪切变换。有两种剪切变换X-Shear和Y-Shear。一个移动 X 坐标值，另一个移动 Y 坐标值。然而; 在这两种情况下，只有一个坐标更改其坐标，而其他坐标则保留其值。剪切也称为倾斜。

X-剪切

X 剪切保留 Y 坐标并对 X 坐标进行更改，这会导致垂直线向右或向左倾斜，如下图所示。

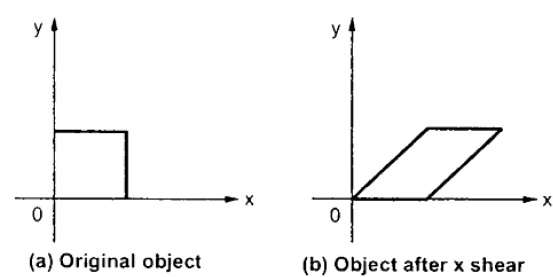
X-Shear 的变换矩阵可以表示为 -

$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

Y' = Y + Sh _y。X

X' = X

Y 剪力

Y 剪切保留 X 坐标并更改 Y 坐标，这会导致水平线转变为向上或向下倾斜的线，如下图所示。

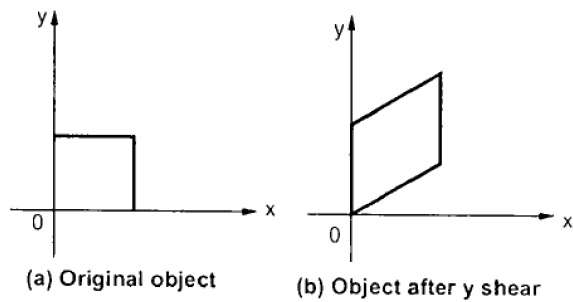
Y 剪切力可以用矩阵表示为 -

$$Y_{sh} \begin{bmatrix} 1& 0& 0\\害羞& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

X' = X + Sh _x。是

Y' = Y

复合变换

如果平面 T1 的变换之后是第二平面变换 T2，则结果本身可以由单个变换 T 表示，该变换 T 是按该顺序采取的 T1 和 T2 的组合。这可写为 T = T1∙T2。

复合变换可以通过变换矩阵的级联获得组合变换矩阵来实现。

组合矩阵 -

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

其中 [Ti] 是以下任意组合

翻译
缩放
剪毛
回转
反射

变换顺序的改变会导致不同的结果，因为一般矩阵乘法不是累积的，即 [A] 。[B] ≠ [B] 。[A] 和乘法顺序。组合变换的基本目的是通过对一个点应用单个组合变换来获得效率，而不是一个接一个地应用一系列变换。

_{例如，要围绕任意点 (X p} , Y _p )旋转对象，我们必须执行三个步骤 -

将点 (X _p , Y _p ) 平移到原点。
绕原点旋转它。
最后，将旋转中心平移回原来的位置。

3D 计算机图形学

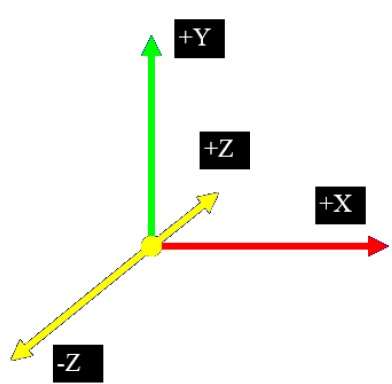
在 2D 系统中，我们仅使用两个坐标 X 和 Y，但在 3D 系统中，添加了一个额外的坐标 Z。3D 图形技术及其应用是娱乐、游戏和计算机辅助设计行业的基础。这是科学可视化的一个持续研究领域。

此外，3D 图形组件现在几乎是每台个人计算机的一部分，尽管传统上用于游戏等图形密集型软件，但它们越来越多地被其他应用程序使用。

平行投影

平行投影会丢弃 z 坐标，并且对象上每个顶点的平行线会延伸，直到与视图平面相交。在平行投影中，我们指定投影方向而不是投影中心。

在平行投影中，投影中心到投影平面的距离是无穷大。在这种类型的投影中，我们通过与原始对象上的连接相对应的线段连接投影的顶点。

平行投影不太现实，但有利于精确测量。在这种类型的投影中，平行线保持平行并且角度不保留。以下层次结构显示了各种类型的平行投影。

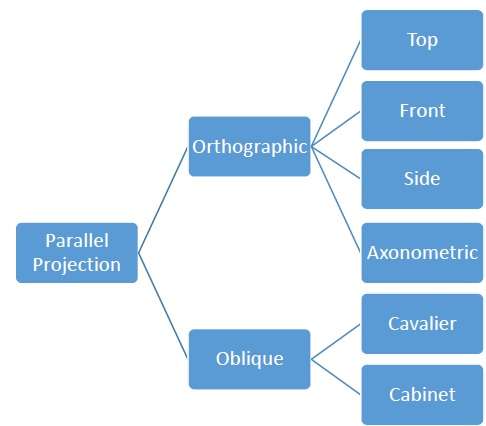
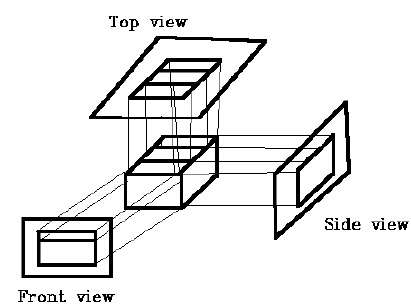
正投影

在正交投影中，投影方向垂直于平面投影。正交投影分为三种类型 -

正投
顶部投影
侧投影

斜投影

在斜投影中，投影方向不垂直于平面投影。在斜投影中，我们可以比正投影更好地观察物体。

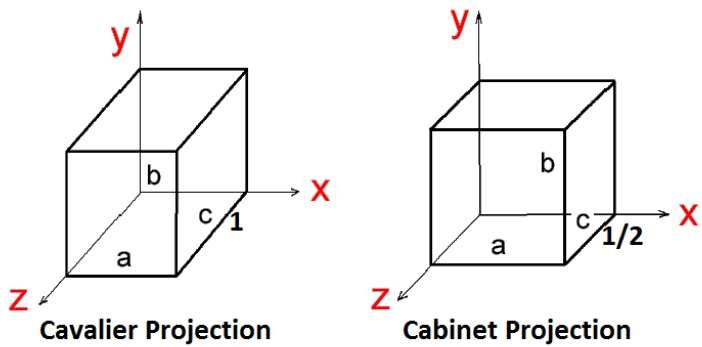
倾斜投影有两种类型 -骑士式和内阁式。Cavalier 投影与投影平面成 45° 角。在骑士投影中，垂直于视平面的线的投影与线本身的长度相同。在骑士投影中，所有三个主方向的透视缩短因子相等。

内阁投影与投影平面成 63.4° 角。在内阁投影中，垂直于观察表面的线以其实际长度的 1/2 进行投影。两个投影如下图所示 -

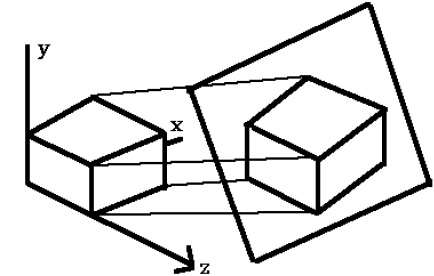
等角投影

显示物体多于一侧的正投影称为轴测正投影。最常见的轴测投影是等角投影，其中投影平面与模型坐标系中的每个坐标轴以相等的距离相交。在该投影中，保留了线的平行度，但不保留角度。下图显示等角投影 -

透视投影

在透视投影中，投影中心到投影平面的距离是有限的，物体的大小与距离成反比，看起来更真实。

距离和角度不会保留，平行线也不会保持平行。相反，它们都汇聚在一个点，称为投影中心或投影参考点。透视投影有 3 种类型，如下图所示。

一点透视投影绘制起来很简单。
两点透视投影可提供更好的深度印象。
三点透视投影是最难画的。

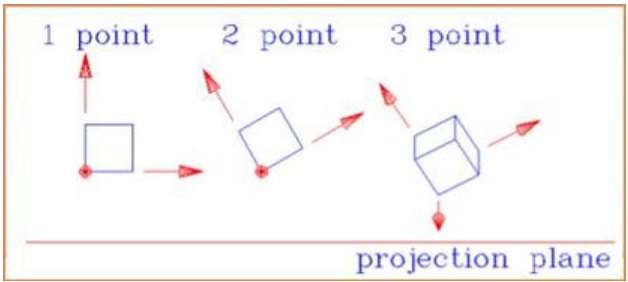
下图显示了所有三种类型的透视投影 -

翻译

在 3D 翻译中，我们将 Z 坐标与 X 和 Y 坐标一起传输。3D 翻译过程与 2D 翻译类似。平移将对象移动到屏幕上的不同位置。

下图展示了翻译后的效果 -

通过将平移坐标 $(t_{x,} t_{y,} t_{z})$ 添加到原始坐标 (X, Y, Z) 来获得新坐标 (X', Y)，可以对点进行 3D 平移'，Z'）。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P' = P∙T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{ bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

3D 变换

回转

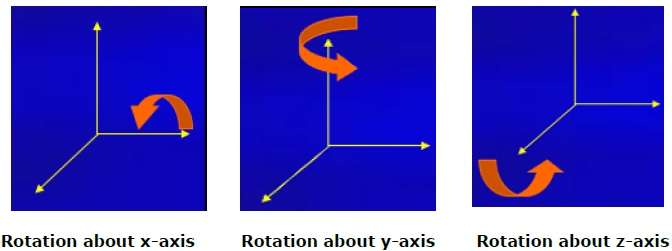
3D 旋转与 2D 旋转不同。在 3D 旋转中，我们必须沿着旋转轴指定旋转角度。我们可以绕 X、Y 和 Z 轴执行 3D 旋转。它们以矩阵形式表示如下 -

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\ \ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

下图解释了绕各个轴的旋转 -

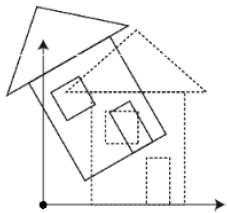
缩放

您可以使用缩放变换来更改对象的大小。在缩放过程中，您可以扩大或压缩对象的尺寸。可以通过将对象的原始坐标乘以缩放因子来实现缩放，以获得所需的结果。下图显示了3D缩放的效果 -

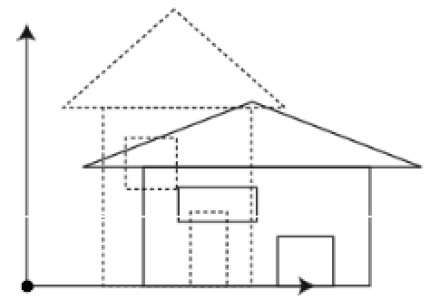
在3D缩放操作中，使用三个坐标。假设原始坐标为(X, Y, Z)，缩放因子分别为$(S_{X,} S_{Y,} S_{z})$，生成的坐标为(X', Y' ，Z'）。这可以用数学方式表示，如下所示 -

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P'=P·S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0&1 \end{b矩阵}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

剪切

使物体形状倾斜的变换称为剪切变换。与 2D 剪切一样，我们可以在 3D 中沿 X 轴、Y 轴或 Z 轴剪切对象。

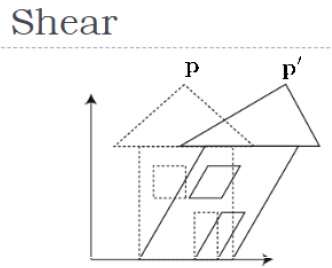
如上图所示，有一个坐标P。你可以剪切它得到一个新的坐标P'，它可以用3D矩阵形式表示如下 -

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P' = P ∙ Sh

$X' = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$

$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$

$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$

变换矩阵

变换矩阵是变换的基本工具。nxm 维的矩阵与对象的坐标相乘。通常使用 3 x 3 或 4 x 4 矩阵进行变换。例如，考虑以下用于各种操作的矩阵。

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
翻译矩阵	缩放矩阵	剪切矩阵
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \结束{b矩阵}$	$R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end {b矩阵}$	$R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \结束{b矩阵}$
旋转矩阵

计算机图形曲线

在计算机图形学中，我们经常需要在屏幕上绘制不同类型的对象。物体并不总是平坦的，我们需要多次绘制曲线才能绘制物体。

曲线类型

曲线是无限大的点集。除端点外，每个点都有两个邻居。曲线可大致分为三类：显式曲线、隐式曲线和参数曲线。

隐式曲线

隐式曲线表示通过使用可以测试曲线上的点是否位于曲线上的过程来定义曲线上的点集。通常，隐式曲线由以下形式的隐式函数定义 -

f(x,y) = 0

它可以表示多值曲线（一个 x 值有多个 y 值）。一个常见的例子是圆，其隐式表示为

x ² + y ² - R ² = 0

显式曲线

数学函数 y = f(x) 可以绘制为曲线。这样的函数是曲线的显式表示。显式表示并不通用，因为它不能表示垂直线并且也是单值的。对于每个 x 值，该函数通常只计算一个 y 值。

参数曲线

具有参数形式的曲线称为参数曲线。仅当函数已知时才能使用显式和隐式曲线表示。在实践中使用参数曲线。二维参数曲线具有以下形式 -

P(t) = f(t), g(t) 或 P(t) = x(t), y(t)

函数 f 和 g 成为曲线上任意点的 (x, y) 坐标，当参数 t 在一定区间 [a, b]（通常为 [0, 1]）内变化时获得这些点。

贝塞尔曲线

贝塞尔曲线是由法国工程师皮埃尔·贝塞尔发现的。这些曲线可以在其他点的控制下生成。使用控制点的近似切线来生成曲线。贝塞尔曲线可以在数学上表示为 -

$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$

其中 $p_{i}$ 是点集，${B_{i}^{n}}(t)$ 表示伯恩斯坦多项式，由下式给出 -

$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{ni}t^{i}$$

其中n是多项式次数，i是索引，t是变量。

最简单的贝塞尔曲线是从点 $P_{0}$ 到 $P_{1}$ 的直线。二次贝塞尔曲线由三个控制点确定。三次贝塞尔曲线由四个控制点确定。

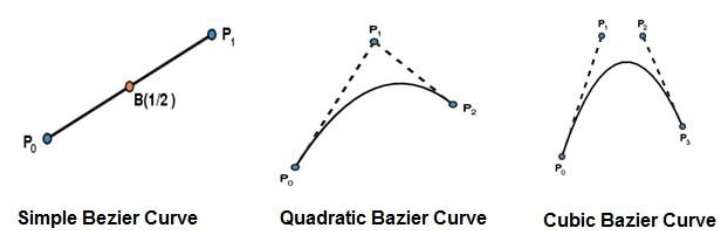
贝塞尔曲线的属性

贝塞尔曲线具有以下属性 -

它们通常遵循控制多边形的形状，控制多边形由连接控制点的线段组成。
他们总是经过第一个和最后一个控制点。
它们包含在其定义控制点的凸包中。
定义曲线段的多项式的次数比定义多边形点的数量减一。因此，对于4个控制点，多项式的次数为3，即三次多项式。
贝塞尔曲线通常遵循定义多边形的形状。
端点处的切向量的方向与由第一段和最后一段线段确定的向量的方向相同。
贝塞尔曲线的凸包属性可确保多项式平滑地遵循控制点。
没有一条直线与贝塞尔曲线相交的次数多于与控制多边形相交的次数。
它们在仿射变换下是不变的。
贝塞尔曲线表现出全局控制意味着移动控制点会改变整个曲线的形状。
给定的贝塞尔曲线可以在点 t=t0 处细分为两个贝塞尔线段，这两个贝塞尔线段在对应于参数值 t=t0 的点处连接在一起。

B 样条曲线

由伯恩斯坦基函数产生的贝塞尔曲线的灵活性有限。

首先，指定多边形顶点的数量固定了定义曲线的所得多项式的阶数。
第二个限制特征是，对于整条曲线上的所有参数值，混合函数的值均不为零。

B 样条基包含 Bernstein 基作为特例。B 样条基础是非全局的。

B 样条曲线定义为控制点 Pi 和 B 样条基函数 $N_{i,}$ k (t) 的线性组合，如下所示

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \ : [ tk-1,tn+1]$

在哪里，

{$p_{i}$: i=0, 1, 2….n} 是控制点
k 是 B 样条曲线的多项式段的阶数。k 阶表示曲线由 k - 1 次的分段多项式段组成，
$N_{i,k}(t)$ 是“标准化 B 样条混合函数”。它们由 k 阶和通常称为“结序列”的非递减实数序列来描述。

$${t_{i}:i = 0, ... n + K}$$

N _i , k 函数描述如下 -

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0 ,& 否则\end{矩阵}\right.$$

如果 k > 1，

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i +k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

和

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

B 样条曲线的属性

B 样条曲线具有以下属性 -

任何参数值的 B 样条基函数之和均为 1。
对于所有参数值，每个基函数都是正值或零。
除 k=1 外，每个基函数都恰好有一个最大值。
曲线的最大阶数等于定义多边形的顶点数。
B样条多项式的次数与定义多边形的顶点数无关。
B 样条允许对曲线表面进行局部控制，因为每个顶点仅在其相关基函数非零的参数值范围内影响曲线的形状。
该曲线表现出变化递减特性。
该曲线通常遵循定义多边形的形状。
任何仿射变换都可以通过将其应用于定义多边形的顶点来应用于曲线。
其定义多边形的凸包内的曲线。

计算机图形表面

多边形表面

对象被表示为表面的集合。3D 对象表示分为两类。

边界表示（B-reps） - 将 3D 对象描述为一组将对象内部与环境分开的表面。
空间分区表示- 它用于通过将包含对象的空间区域划分为一组小的、不重叠的、连续的实体（通常是立方体）来描述内部属性。

3D 图形对象最常用的边界表示是一组包围对象内部的表面多边形。许多图形系统都使用这种方法。存储一组多边形用于对象描述。这简化并加速了对象的表面渲染和显示，因为所有表面都可以用线性方程描述。

多边形表面在设计和实体建模应用中很常见，因为它们的线框显示可以快速完成以给出表面结构的一般指示。然后通过在多边形表面上插入阴影图案来照明来产生逼真的场景。

多边形表

在此方法中，表面由一组顶点坐标和关联属性指定。如下图所示，有五个顶点，从 v ₁到 v ₅。

每个顶点存储x、y和z坐标信息，在表中表示为v ₁ : x ₁ , y ₁ , z ₁。
边表用于存储多边形的边信息。在下图中，边 E ₁位于